Capítulo 2 - Organização, visualização e descrição de dados

# !pip install -r requirements.txt

Tipos de dados

Os dados podem ser definidos como uma colecção de dados de painel, caracteres, palavras e texto, assim como imagens, áudio, vídeo, etc. Para escolher os métodos estatísticos apropriados para resumir e analisar dados e seleccionar gráficos adequados para visualizar dados, precisamos distinguir entre os diferentes tipos de dados.

Dados númericos

Dados numéricos são valores que representam quantidades que podem ser medidas ou contadas como um número (também podem ser chamados de dados quantitativos). Os dados numéricos (quantitativos) podem ser divididos em dois tipos: dados discretos ou contínuos.

Dados discretos são valores numéricos que resultam de um processo de contagem. Assim, praticamente falando, os dados são limitados a um número finito de valores. Por exemplo o número de anos até à reforma.

Dados contínuos são dados que podem ser medidos e podem assumir qualquer valor num intervalo especifico de valores. Por exemplo, os retornos de preço de uma acção.

Dados categóricos

Dados categóricos (também podem ser chamados de dados qualitativos) são valores que descrevem uma qualidade ou característica de um grupo de observações e, portanto, podem ser usados como rótulos para dividir um conjunto de dados em grupos para resumir e visualizar. Normalmente podem apenas ser um número limitado de valores que são mutuamente exclusivos.

Dados nominais são valores categóricos que não são passíveis de serem organizados numa ordem lógica. Por exemplo os sectores no S&P 500. Tecnologia de informação, energia, retalho, etc.

Dados ordinais são valores categóricos que podem ser ordenados ou classificados logicamente. Por exemplo, as estrelas Morningstar (para os fundos).

Exercício 2.1

Identifique o tipo de dados nos seguintes exemplos:

• Número de pagamentos de cupões numa obrigação

• Montante dos dividendos de uma acção cotada em bolsa

• Ratings de crédito de obrigações

• Classificações de estilo de hedge funds

Resolução:

• Dados numéricos discretos. Os cupões a pagar podem ser 9, 10, 11 etc

• Dados numéricos contínuos. Pode ser um dividendo de 1 euros, 2 euros ou qualquer valor no meio. Teoricamente há uma quantidade infinita de valores.

• Dados categóricos ordinais. O rating pode ser, no caso da Standard and Poor’s, AAA, AA, B, C etc. A questão é que se pode ordenar do maior rating para o mais baixo.

• Dados categóricos nominais. Há várias estratégias e hedge funds que se especializam nelas: Long/Short Equity, Market Neutral, Merger Arbitrage, Convertible Arbitrage. Isso nada nos diz sobre a qualidade dos mesmos e nem podemos ordenar por qualidade.

Dados Transversais versus séries temporais vs dados de painel

Outro padrão de classificação de dados é baseado em como os dados são recolhidos e categoriza os dados em três tipos: transversais, série temporal e painel.

Para melhor percebermos os este ponto devemos também saber distinguir uma variável de uma observação. Uma variável é uma característica ou quantidade que pode ser medida, contado ou categorizado e está sujeito a alterações. A variável também pode ser denominada atributo. Por seu lado uma observação é o valor de uma variável específica num ponto no tempo ou ao longo de um período de tempo especificado.

Os dados transversais são uma lista das observações de uma variável específica de várias unidades observacionais num determinado ponto no tempo;

As séries temporais é uma sequência de observações para uma única unidade observacional de uma variável específica ao longo do tempo e em intervalos discretos, tipicamente igualmente espaçados no tempo;

Os dados do painel são uma mistura de séries temporais e dados transversais que são frequentemente usado na análise e modelagem financeira.

Exercício 2.2

O quadro seguinte representa a performance de 3 índices ao longo de 4 anos

Responda se os pontos seguintes podem ser melhor categorizados por serem dados de painel, séries-temporais ou

1. Cada coluna da tabela;

2. Cada linha da tabela;

3. A tabela como um todo.

Resolução

1. Série temporal. Sequência de observações de um índice ao longo do tempo.

2. Dados transversais. São uma lista das observações de uma variável específica (retorno) de várias unidades observacionais (índices) num determinado ponto no tempo (apenas naquele ano);

3. Dados de painel. Pois inclui uma mistura de dados temporais e transversais.

Dados estruturados vs dados não estruturados

Os dados estruturados são dados organizados de maneira pré-definida, geralmente repetindo padrões. As formas típicas de dados estruturados são normalmente arrays unidimensionais, como uma série temporal, ou tabelas de dados bidimensionais, onde cada coluna representa uma variável ou uma unidade de observação e cada linha contém um conjunto de valores para as mesmas colunas.

Os dados não estruturados, por outro lado, não seguem nenhuma forma de organização convencional. Alguns tipos comuns de dados não estruturados são texto - como informações financeiras ou notícias - mas também áudio, vídeo ou imagens.

Dados não estruturado são tipicamente dados alternativos, pois geralmente são criados através de fontes recentes (social media) e/ou não convencionais (fotos em massa tiradas por satélites).

Exercício 2.3

Qual dos seguintes é mais provável de ser dados estruturados?

1. Publicações de social media onde os consumidores estão a comentar sobre o que pensam de um novo produto.

2. Preços de fecho diários durante o mês passado para todas as empresas listadas na Índice de acções Nikkei 225 do Japão.

3. Áudio e vídeo de um CFO comunicando os últimos ganhos da empresa aos analistas.

2. O preço de fecho diários de cotações de empresas é um exemplo de dados altamente estruturados. A e B são exemplo de dados não estruturados.

Organização de dados para análise quantitativa

A análise quantitativa normalmente exige que os dados estejam em um formato limpo e de forma formatada, portanto, os dados brutos geralmente não são adequados para uso directo por analistas.

Dependendo do número de variáveis, os dados brutos podem ser organizados em dois formatos típicos para análise quantitativa: arrays unidimensionais e matrizes bidimensionais rectangulares.

Um array unidimensional é o formato mais simples para representar uma colecção de dados do mesmo tipo de dados, portanto, é adequado para representar uma única variável. Ex: Cotações diárias de uma acção em 2021.

Uma matriz bidimensional rectangular (também chamada de tabela de dados) é uma das mais formas populares de organização de dados para processamento por computadores ou para apresentação de dados visualmente para consumo humano. Semelhante à estrutura em uma folha de Excel, uma tabela de dados é composta de colunas e linhas para conter múltiplas variáveis e múltiplas observações, respectivamente.

Exemplo:

Dados em bruto

Transformação para datatable de forma a usar em modelos

Este tipo de transformação é algo que se vê em modelos de machine learning.

Resumir dados usando tabelas de frequência

Uma distribuição de frequência é uma exibição de dados construídos contando as observações de uma variável por valores distintos ou grupos e somando os valores de uma variável numérica num tabela ordenada. É uma ferramenta importante para inicialmente resumir dados por grupos ou compartimentos para uma interpretação mais fácil.

Frequência absoluta e frequência relativa

A frequência absoluta, ou simplesmente a frequência bruta, é o número real de observações contadas para cada valor único da variável (ou seja, cada sector).

Mas muitas vezes é também desejável expressar as frequências em termos de percentagens, então também mostramos a frequência relativa, que é calculada como a frequência absoluta de cada valor único da variável dividido pelo número total de observações. A frequência relativa fornece uma medida normalizada da distribuição dos dados, permitindo comparações entre conjuntos de dados com diferentes números de observações totais.

A frequência absoluta, ou simplesmente a frequência bruta, é o número real de observações contadas para cada valor único da variável (ou seja, cada sector).

Mas muitas vezes é também desejável expressar as frequências em termos de percentagens, então também mostramos a frequência relativa, que é calculada como a frequência absoluta de cada valor único da variável dividido pelo número total de observações. A frequência relativa fornece uma medida normalizada da distribuição dos dados, permitindo comparações entre conjuntos de dados com diferentes números de observações totais.

Uma tabela de distribuição de frequência fornece uma visão dos dados e facilita encontrar padrões.

Um procedimento para construir uma distribuição de frequência para dados numéricos pode ser da seguinte forma:

1. Classifique os dados em ordem crescente.

2. Calcule a dispersão dos dados, definida como Faixa = Valor máximo − Valor mínimo.

3. Decida o número de bins/compartimentos (k) na distribuição de frequência.

4. Determine a largura do compartimento como Faixa/k.

5. Determine o número de observações que caem em cada compartimento contando as número de observações cujos valores são iguais ou superiores ao mínimo do compartimento.

6. Construa uma tabela dos compartimentos listados do menor para o maior que mostre o número de observações que caem em cada compartimento.

Exercício 2.4

O quadro seguinte representa a performance dos índices accionistas de vários países em determinado ano. Construa uma tabela de distribuição e frequência com estes dados.

Resolução

import pandas as pd

url = "https://s3.us-east-2.amazonaws.com/cbs.pg.repository/data/example_4.xlsx"
df = pd.read_excel(url)[['Mercado', 'Retorno (%)']].dropna()
df

	Mercado	Retorno (%)
0	País A	7.7
1	País B	8.5
2	País C	9.1
3	País D	5.5
4	País E	7.1
5	País F	9.9
6	País G	6.2
7	País H	6.8
8	País I	7.5
9	País J	8.9
10	País K	7.4
11	País L	8.6
12	País M	9.6
13	País N	7.7
14	País O	6.8
15	País P	6.1
16	País R	8.8
17	País Q	7.9

df_sorted = df.sort_values(by='Retorno (%)', ascending=False)
df_sorted

	Mercado	Retorno (%)
5	País F	9.9
12	País M	9.6
2	País C	9.1
9	País J	8.9
16	País R	8.8
11	País L	8.6
1	País B	8.5
17	País Q	7.9
13	País N	7.7
0	País A	7.7
8	País I	7.5
10	País K	7.4
4	País E	7.1
7	País H	6.8
14	País O	6.8
6	País G	6.2
15	País P	6.1
3	País D	5.5

df_range = df['Retorno (%)'].max() - df['Retorno (%)'].min()
df_range

4.4

k = 5

Bin_width= df_range / k
round(Bin_width, 2)

0.88

Vamos usar 1, por arredondamento

Criando fórmula python para fazer o quadro:

def create_frequency_table(data, bins, column):
    df = pd.DataFrame(data[column]).groupby(pd.cut(data[column], bins)).count()
    df.columns = ['Frequência Absoluta']
    df['Frequência relativa (%)'] = round(df['Frequência Absoluta'] /
                                    df['Frequência Absoluta'].sum() * 100, 2)
    df['Frequência Absoluta acumulada'] = df['Frequência Absoluta'].cumsum()
    df['Frequência relativa acumulada (%)'] =  round(df['Frequência Absoluta acumulada'] / len(data), 4) * 100
    return df

tf = create_frequency_table(df, bins = [5, 6, 7, 8, 9, 10], column='Retorno (%)')
tf

/tmp/ipykernel_158640/4227145889.py:2: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df = pd.DataFrame(data[column]).groupby(pd.cut(data[column], bins)).count()

	Frequência Absoluta	Frequência relativa (%)	Frequência Absoluta acumulada	Frequência relativa acumulada (%)
Retorno (%)
(5, 6]	1	5.56	1	5.56
(6, 7]	4	22.22	5	27.78
(7, 8]	6	33.33	11	61.11
(8, 9]	4	22.22	15	83.33
(9, 10]	3	16.67	18	100.00

Curiosidade: Fazer uma tabela de frequência com as rentabilidades mensais do SPY (ETF S&P 500)

Funções python que vamos precisar:

#pip install yfinance
import yfinance as yf

def merge_time_series(df_1, df_2, how='outer'):
    df = df_1.merge(df_2, how=how, left_index=True, right_index=True)
    return df

def normalize(df):
    df = df.dropna()
    return (df / df.iloc[0]) * 100

def download_yahoo_data(tickers, normalize_quotes=False,
                      start='1970-01-01', end='2030-12-31'):
    quotes=pd.DataFrame()
    for ticker in tickers:
        df = yf.download(ticker, start=start, end=end, progress=False)
        df = df[['Adj Close']]
        df.columns=[ticker]
        quotes = merge_time_series(quotes, df)
    
    quotes = quotes.ffill()
     
    if normalize_quotes:
        quotes = normalize(quotes)

    return quotes

Download das cotações do S&P 500 deste século e fazer a dataframe com as rentabilidades mensais

# Download das cotações do S&P 500 deste século
SPY = download_yahoo_data(tickers=['SPY'], start='1999-12-31', end='2021-12-31')

# Fazer resample para dados mensais (ir buscar o último dado do mês)
SPY_mensal = SPY.resample('M').last()

# Calcular retornos em percentagem com a função ptc_change()
SPY_mensal_ret = SPY_mensal.pct_change().dropna()

# Dar o nome de S&P Ret à coluna
SPY_mensal_ret.columns = ['SPY']

# Transformar em percentagens
SPY_mensal_ret = SPY_mensal_ret * 100

# Mostrar o DataFrame
SPY_mensal_ret

/tmp/ipykernel_158640/2106034703.py:5: FutureWarning: 'M' is deprecated and will be removed in a future version, please use 'ME' instead.
  SPY_mensal = SPY.resample('M').last()

	SPY
Date
2000-01-31	-4.978723
2000-02-29	-1.522623
2000-03-31	9.691470
2000-04-30	-3.512029
2000-05-31	-1.572294
...	...
2021-08-31	2.975976
2021-09-30	-4.660530
2021-10-31	7.016357
2021-11-30	-0.803484
2021-12-31	4.889113

264 rows × 1 columns

Encontrar o mínimo:

# Ver qual o retorno mínimo do S&P para fazermos a tabela de frequência
SPY_mensal_ret.min()

SPY   -16.518677
dtype: float64

Encontrar o máximo:

# Ver qual o retorno máximo do S&P para fazermos a tabela de frequência
SPY_mensal_ret.max()

SPY    12.698323
dtype: float64

Tabela de frequência dos retornos mensais de SPY

import numpy as np
# Criar tabela de frequência do SPY
SPY_tb = create_frequency_table(SPY_mensal_ret,
                              bins = np.arange(-17, 14),
                              column='SPY')
SPY_tb

/tmp/ipykernel_158640/4227145889.py:2: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  df = pd.DataFrame(data[column]).groupby(pd.cut(data[column], bins)).count()

	Frequência Absoluta	Frequência relativa (%)	Frequência Absoluta acumulada	Frequência relativa acumulada (%)
SPY
(-17, -16]	1	0.38	1	0.38
(-16, -15]	0	0.00	1	0.38
(-15, -14]	0	0.00	1	0.38
(-14, -13]	0	0.00	1	0.38
(-13, -12]	1	0.38	2	0.76
(-12, -11]	0	0.00	2	0.76
(-11, -10]	2	0.76	4	1.52
(-10, -9]	2	0.76	6	2.27
(-9, -8]	4	1.52	10	3.79
(-8, -7]	5	1.89	15	5.68
(-7, -6]	7	2.65	22	8.33
(-6, -5]	7	2.65	29	10.98
(-5, -4]	4	1.52	33	12.50
(-4, -3]	9	3.41	42	15.91
(-3, -2]	12	4.55	54	20.45
(-2, -1]	26	9.85	80	30.30
(-1, 0]	17	6.44	97	36.74
(0, 1]	29	10.98	126	47.73
(1, 2]	37	14.02	163	61.74
(2, 3]	28	10.61	191	72.35
(3, 4]	25	9.47	216	81.82
(4, 5]	14	5.30	230	87.12
(5, 6]	10	3.79	240	90.91
(6, 7]	9	3.41	249	94.32
(7, 8]	3	1.14	252	95.45
(8, 9]	7	2.65	259	98.11
(9, 10]	2	0.76	261	98.86
(10, 11]	2	0.76	263	99.62
(11, 12]	0	0.00	263	99.62
(12, 13]	1	0.38	264	100.00

---

Visualização de Dados

A visualização é a apresentação de dados em formato gráfico com o propósito de aumentar a compreensão e obter insights sobre os dados. Como tem já foi dito que “uma imagem vale mais que mil palavras”. Nesta secção, discutimos uma variedade de gráficos que são úteis para entender distribuições, fazer comparações e explorando relacionamentos potenciais entre dados.

---

Histograma

Um histograma é um gráfico que apresenta a distribuição de dados numéricos usando a altura de uma barra ou coluna para representar a frequência absoluta ou relativa de cada bin ou intervalo na distribuição.

Continuando com o exemplo de rentabilidades mensais do SPY:

# Referência: https://towardsdatascience.com/histograms-with-plotly-express-complete-guide-d483656c5ad7
# Referência: https://plotly.com/python/histograms/
# https://colab.research.google.com/github/amadords/Projetos-Publicos/blob/master/Introdu%C3%A7%C3%A3o_ao_Plotly.ipynb#scrollTo=EUXzRF0ABxqY

import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('seaborn-v0_8')

# Define the plot size
plt.figure(figsize=(10, 5))

# Create the histogram
sns.histplot(
    data=SPY_mensal_ret, 
    x="SPY", 
    kde=False, 
    edgecolor="whitesmoke", 
    linewidth=1
)

# Set plot titles and labels
plt.title("Histograma (absoluto) dos retornos mensais do S&P 500")
plt.xlabel("Variações em percentagem")
plt.ylabel("Valores absolutos")

# Show the plot
plt.show()

# Set the plot size
plt.figure(figsize=(10, 5))

# Create the normalized histogram (probability density)
sns.histplot(
    data=SPY_mensal_ret, 
    x="SPY", 
    stat="density",  # Equivalent to 'histnorm=probability density'
    kde=False, 
    edgecolor="whitesmoke", 
    linewidth=1
)

# Set plot titles and labels
plt.title("Histograma (relativo) dos retornos mensais do S&P 500")
plt.xlabel("Variações em percentagem")
plt.ylabel("Valores relativos")

# Format the y-axis as percentages
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda y, _: f'{y:.0%}'))

# Show the plot
plt.show()

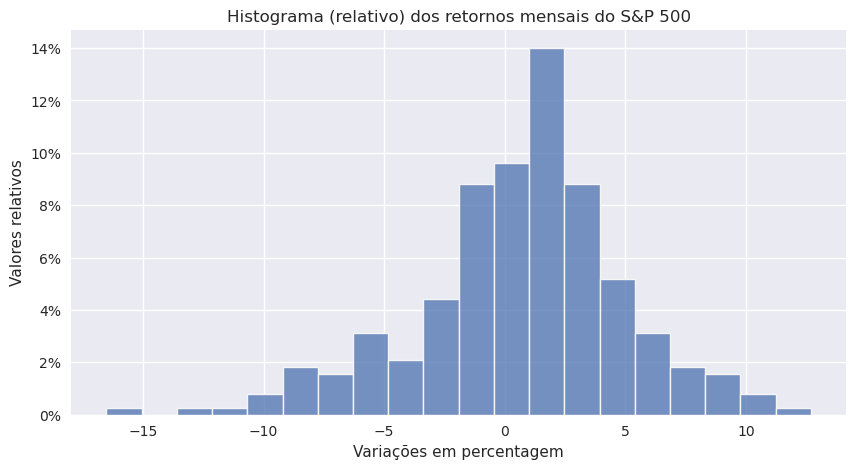
Podemos comparar os valores nos gráficos com a tabela de frequência.

---

Gráfico de barras

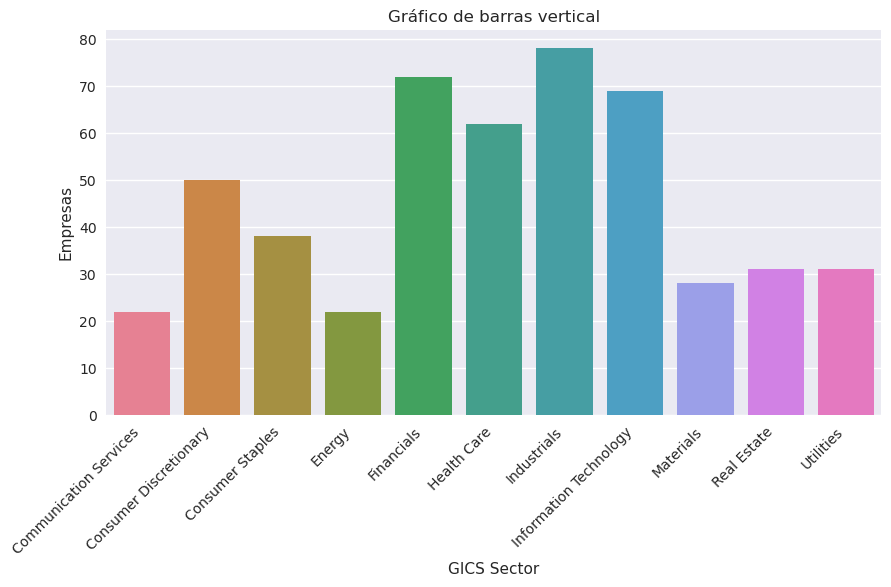
Como demonstramos, o histograma é uma ferramenta gráfica eficiente para apresentar a distribuição de frequência de dados numéricos. A distribuição de frequência de categóricos os dados um tipo semelhante de gráfico chamado gráfico de barras. Em um gráfico de barras, cada bar representa uma categoria distinta, com a altura da barra proporcional à frequência da categoria correspondente.

Extra (ir buscar os sectores das acções do S&P 500 à Wikipedia)

# Ir buscar a tabela das acções
url = "https://en.wikipedia.org/wiki/List_of_S%26P_500_companies"
Sector = pd.read_html(url)[0]
Sector

	Symbol	Security	GICS Sector	GICS Sub-Industry	Headquarters Location	Date added	CIK	Founded
0	MMM	3M	Industrials	Industrial Conglomerates	Saint Paul, Minnesota	1957-03-04	66740	1902
1	AOS	A. O. Smith	Industrials	Building Products	Milwaukee, Wisconsin	2017-07-26	91142	1916
2	ABT	Abbott Laboratories	Health Care	Health Care Equipment	North Chicago, Illinois	1957-03-04	1800	1888
3	ABBV	AbbVie	Health Care	Biotechnology	North Chicago, Illinois	2012-12-31	1551152	2013 (1888)
4	ACN	Accenture	Information Technology	IT Consulting & Other Services	Dublin, Ireland	2011-07-06	1467373	1989
...	...	...	...	...	...	...	...	...
498	XYL	Xylem Inc.	Industrials	Industrial Machinery & Supplies & Components	White Plains, New York	2011-11-01	1524472	2011
499	YUM	Yum! Brands	Consumer Discretionary	Restaurants	Louisville, Kentucky	1997-10-06	1041061	1997
500	ZBRA	Zebra Technologies	Information Technology	Electronic Equipment & Instruments	Lincolnshire, Illinois	2019-12-23	877212	1969
501	ZBH	Zimmer Biomet	Health Care	Health Care Equipment	Warsaw, Indiana	2001-08-07	1136869	1927
502	ZTS	Zoetis	Health Care	Pharmaceuticals	Parsippany, New Jersey	2013-06-21	1555280	1952

503 rows × 8 columns

# Agregar por GICS Sector
GICS_sector = Sector.groupby('GICS Sector').count()
GICS_sector

	Symbol	Security	GICS Sub-Industry	Headquarters Location	Date added	CIK	Founded
GICS Sector
Communication Services	22	22	22	22	22	22	22
Consumer Discretionary	50	50	50	50	50	50	50
Consumer Staples	38	38	38	38	38	38	38
Energy	22	22	22	22	22	22	22
Financials	72	72	72	72	72	72	72
Health Care	62	62	62	62	62	62	62
Industrials	78	78	78	78	78	78	78
Information Technology	69	69	69	69	69	69	69
Materials	28	28	28	28	28	28	28
Real Estate	31	31	31	31	31	31	31
Utilities	31	31	31	31	31	31	31

# Set the plot size
plt.figure(figsize=(10, 5))

# Create the bar plot
sns.barplot(
    x=GICS_sector.index, 
    y=GICS_sector['Symbol'], 
    palette='husl'  # Change this to another palette if desired
)

# Set plot titles and labels
plt.title("Gráfico de barras vertical")
plt.xlabel("GICS Sector")
plt.ylabel("Empresas")

# Rotate x-axis labels for better readability
plt.xticks(rotation=45, ha='right')

# Show the plot
plt.show()

/tmp/ipykernel_158640/71999995.py:5: FutureWarning: 

Passing `palette` without assigning `hue` is deprecated and will be removed in v0.14.0. Assign the `x` variable to `hue` and set `legend=False` for the same effect.

  sns.barplot(

---

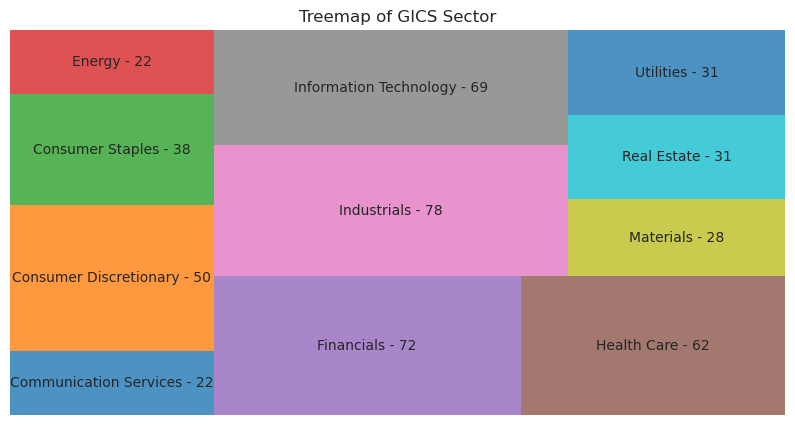
Mapa de árvore

Além de gráficos de barras e gráficos de barras agrupados, outra ferramenta gráfica para exibir os dados categóricos são um mapa de árvore. Consiste em um conjunto de rectângulos coloridos para representar grupos distintos, e a área de cada rectângulo é proporcional ao valor do grupo correspondente.

import matplotlib.pyplot as plt
import squarify

# Generate labels for the Treemap
labels_names = [f"{GICS_sector.index[i]} - {GICS_sector['Symbol'][i]}" for i in range(len(GICS_sector))]

# Define values and labels for the Treemap
values = list(GICS_sector['Symbol'])
labels = labels_names

import matplotlib.pyplot as plt
import squarify

# Plot using a qualitative colormap
plt.figure(figsize=(10, 5))
squarify.plot(
    sizes=values, 
    label=labels, 
    alpha=.8, 
    color=plt.cm.tab10.colors  # Using a qualitative colormap for diverse colors
)

plt.title("Treemap of GICS Sector")
plt.axis('off')
plt.show()

/tmp/ipykernel_158640/1609183072.py:5: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  labels_names = [f"{GICS_sector.index[i]} - {GICS_sector['Symbol'][i]}" for i in range(len(GICS_sector))]

print(plt.colormaps())

['magma', 'inferno', 'plasma', 'viridis', 'cividis', 'twilight', 'twilight_shifted', 'turbo', 'Blues', 'BrBG', 'BuGn', 'BuPu', 'CMRmap', 'GnBu', 'Greens', 'Greys', 'OrRd', 'Oranges', 'PRGn', 'PiYG', 'PuBu', 'PuBuGn', 'PuOr', 'PuRd', 'Purples', 'RdBu', 'RdGy', 'RdPu', 'RdYlBu', 'RdYlGn', 'Reds', 'Spectral', 'Wistia', 'YlGn', 'YlGnBu', 'YlOrBr', 'YlOrRd', 'afmhot', 'autumn', 'binary', 'bone', 'brg', 'bwr', 'cool', 'coolwarm', 'copper', 'cubehelix', 'flag', 'gist_earth', 'gist_gray', 'gist_heat', 'gist_ncar', 'gist_rainbow', 'gist_stern', 'gist_yarg', 'gnuplot', 'gnuplot2', 'gray', 'hot', 'hsv', 'jet', 'nipy_spectral', 'ocean', 'pink', 'prism', 'rainbow', 'seismic', 'spring', 'summer', 'terrain', 'winter', 'Accent', 'Dark2', 'Paired', 'Pastel1', 'Pastel2', 'Set1', 'Set2', 'Set3', 'tab10', 'tab20', 'tab20b', 'tab20c', 'grey', 'gist_grey', 'gist_yerg', 'Grays', 'magma_r', 'inferno_r', 'plasma_r', 'viridis_r', 'cividis_r', 'twilight_r', 'twilight_shifted_r', 'turbo_r', 'Blues_r', 'BrBG_r', 'BuGn_r', 'BuPu_r', 'CMRmap_r', 'GnBu_r', 'Greens_r', 'Greys_r', 'OrRd_r', 'Oranges_r', 'PRGn_r', 'PiYG_r', 'PuBu_r', 'PuBuGn_r', 'PuOr_r', 'PuRd_r', 'Purples_r', 'RdBu_r', 'RdGy_r', 'RdPu_r', 'RdYlBu_r', 'RdYlGn_r', 'Reds_r', 'Spectral_r', 'Wistia_r', 'YlGn_r', 'YlGnBu_r', 'YlOrBr_r', 'YlOrRd_r', 'afmhot_r', 'autumn_r', 'binary_r', 'bone_r', 'brg_r', 'bwr_r', 'cool_r', 'coolwarm_r', 'copper_r', 'cubehelix_r', 'flag_r', 'gist_earth_r', 'gist_gray_r', 'gist_heat_r', 'gist_ncar_r', 'gist_rainbow_r', 'gist_stern_r', 'gist_yarg_r', 'gnuplot_r', 'gnuplot2_r', 'gray_r', 'hot_r', 'hsv_r', 'jet_r', 'nipy_spectral_r', 'ocean_r', 'pink_r', 'prism_r', 'rainbow_r', 'seismic_r', 'spring_r', 'summer_r', 'terrain_r', 'winter_r', 'Accent_r', 'Dark2_r', 'Paired_r', 'Pastel1_r', 'Pastel2_r', 'Set1_r', 'Set2_r', 'Set3_r', 'tab10_r', 'tab20_r', 'tab20b_r', 'tab20c_r', 'rocket', 'rocket_r', 'mako', 'mako_r', 'icefire', 'icefire_r', 'vlag', 'vlag_r', 'flare', 'flare_r', 'crest', 'crest_r']

---

Nuvem de palavras

Até agora, mostramos como visualizar a distribuição de frequência de dados numéricos ou dados categóricos. No entanto, podemos encontrar um gráfico para descrever a frequência de dados não estruturados – particularmente, dados textuais numa nuvem de palavras. Uma nuvem de plavras é uma dispositivo visual para representar dados textuais e consiste em palavras extraídas de uma fonte de dados textuais, com o tamanho de cada palavra distinta sendo proporcional à frequência com que aparece no texto dado.

Nomination_hearing_Jerome_Powell = '''Chairman Brown, Ranking Member Toomey, and 
other members of the Committee, thank you for the opportunity to appear before you
today. I would like to thank President Biden for nominating me to serve a second
term as Chair of the Board of Governors of the Federal Reserve System. I would also
like to thank my colleagues throughout the Federal Reserve System for their education,
perseverance, and tireless work on behalf of the American people. Their commitment
and expertise were essential to the Fed's response to the COVID-19  risis and remain
vital to the implementation of monetary policy as our economy continues to progress.
Particular thanks go to my wife, Elissa Leonard, and our three children, Susie,
Lucy, and Sam. Their love and support make possible everything I do. My five siblings
are all watching, and we are thinking of each other and of our parents today with
love and gratitude. Four years ago, when I sat before this Committee, few could
have predicted the great challenges that would soon become ours to meet. On the eve
of the pandemic, the U.S. economy was enjoying its 11th year of expansion, the
longest on record. Unemployment was at 50-year lows, and the economic benefits were
reaching those most on the margins. No obvious financial or economic imbalances
threatened the ongoing expansion. But this attractive picture turned virtually
overnight as the virus swept across the globe. 

The initial contraction was the fastest and deepest on record, but the pain could
have been much worse. As the pandemic arrived, our immediate challenge was to stave
off a full-scale depression, which would require swift and strong policy actions
from across government. Congress provided by far the fastest and largest response
to any postwar economic downturn. At the Federal Reserve, we used the full range
of policy tools at our disposal. We moved quickly to restore vital flows of credit
to households, communities, and businesses and to stabilize the financial system.
These collective policy actions, the development and availability of vaccines, and
American resilience worked in concert, first to cushion the pandemic's economic blows
and then to spark a historically strong recovery.

Today the economy is expanding at its fastest pace in many years, and the labor
market is strong. As always, challenges remain. Both the initial shutdown and the
subsequent reopening of the economy were without precedent. The economy has
rapidly gained strength despite the ongoing pandemic, giving rise to persistent
supply and demand imbalances and bottlenecks, and thus to elevated inflation. We
know that high inflation exacts a toll, particularly for those less able to meet
the higher costs of essentials like food, housing, and transportation. We are
strongly committed to achieving our statutory goals of maximum employment and
price stability. We will use our tools to support the economy and a strong labor
market and to prevent higher inflation from becoming entrenched. We can begin to
see that the post-pandemic economy is likely to be different in some respects. The
pursuit of our goals will need to take these differences into account. To that end,
monetary policy must take a broad and forward-looking view, keeping pace with an
ever-evolving economy.

Over the past four years, my colleagues and I have continued the work of our
predecessors to ensure a strong and resilient financial system. We increased
capital and liquidity requirements for the largest banks—and currently, capital
and liquidity levels at our largest, most systemically important banks are at
multidecade highs. We worked to improve the public's access to instant payments,
intensified our focus and supervisory efforts on evolving threats such as climate
change and cyberattacks, and expanded our analysis and monitoring of financial
stability. We will remain vigilant about new and emerging threats.
We also updated our monetary policy framework, drawing on insights from people
and communities across the country, to reflect the challenges of conducting policy
in an era of persistently low interest rates.

Congress has assigned the Federal Reserve important goals and has given us
considerable independence in using our tools to achieve them. In our democratic
system, that independence comes with the responsibility of transparency and clear
communication, to keep the public informed and enable effective legislative
oversight. That duty takes on even greater significance when the Fed must
take extraordinary actions in times of crisis. In order to facilitate that
transparency, and to earn your trust and that of the American people, I have
made it a priority to meet regularly and frequently with you and your elected
colleagues. I commit to continuing that practice if I am confirmed to another term.

The Federal Reserve works for all Americans. We know our decisions matter to
every person, family, business, and community across the country. I am committed
to making those decisions with objectivity, integrity, and impartiality,
based on the best available evidence, and in the long-standing tradition of
monetary policy independence. That pledge lies at the heart of the Fed's mission
and is one we all make when we answer the call to public service. I make it here
again, with force and without reservation.
Everything we do at the Federal Reserve is in pursuit of the goals set for us by
Congress. I am honored to have worked in service to those ends since I joined the
Fed in 2012, and as Chair for the past four years.
Thank you. I look forward to your questions'''

# Pode ser encontrado aqui:
# https://www.federalreserve.gov/newsevents/testimony/powell20220111a.htm

import matplotlib.pyplot as plt
from wordcloud import WordCloud
# Start with one review:
text = Nomination_hearing_Jerome_Powell

# Create and generate a word cloud image:
wordcloud = WordCloud(background_color="whitesmoke",
                      width=800,
                      height=400).generate(text)

# Display the generated image:
plt.imshow(wordcloud, interpolation='bilinear')
plt.axis("off")

plt.show()

---

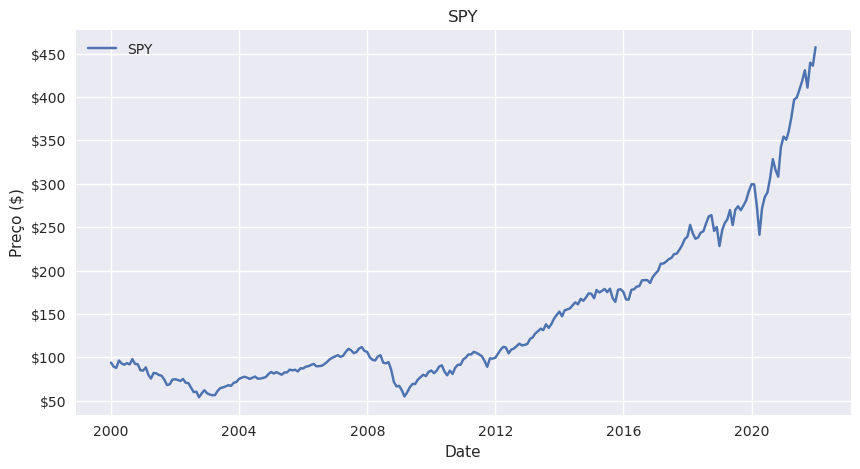
Gráfico de linha

Um gráfico de linhas é um tipo de gráfico usado para visualizar observações ordenadas. Muitas vezes um gráfico de linha é usado para exibir a mudança da série de dados ao longo do tempo (série temporal).

Pegando no exemplo das cotações mensais de SPY que já fizemos o download em cima:

SPY_mensal

	SPY
Date
1999-12-31	93.924156
2000-01-31	89.247932
2000-02-29	87.889023
2000-03-31	96.406761
2000-04-30	93.020927
...	...
2021-08-31	430.711884
2021-09-30	410.638428
2021-10-31	439.450287
2021-11-30	435.919373
2021-12-31	457.231964

265 rows × 1 columns

import matplotlib.pyplot as plt

# Set the plot size
plt.figure(figsize=(10, 5))

# Plot the line chart
plt.plot(SPY_mensal.index, SPY_mensal['SPY'], label='SPY')

# Set plot titles and labels
plt.title("SPY")
plt.xlabel("Date")
plt.ylabel("Preço ($)")

# Customize the y-axis to show dollar symbols
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'${x:,.0f}'))

# Add a legend
plt.legend()

# Show the plot
plt.show()

# Download de SPY (S&P 500) e QQQ (NASDAQ)
ETFs = download_yahoo_data(['SPY', 'QQQ'], start='1999-12-31', end='2021-12-31')

# Resample para business month
# (seleccionando o último preço de cada dia útil do mês)
ETFs_mensal = ETFs.resample('BM').last()
ETFs_mensal

/tmp/ipykernel_158640/705990504.py:6: FutureWarning: 'BM' is deprecated and will be removed in a future version, please use 'BME' instead.
  ETFs_mensal = ETFs.resample('BM').last()

	SPY	QQQ
Date
1999-12-31	93.924156	77.694092
2000-01-31	89.247932	76.259216
2000-02-29	87.889023	90.767082
2000-03-31	96.406761	93.105331
2000-04-28	93.020927	80.563782
...	...	...
2021-08-31	430.711884	372.081635
2021-09-30	410.638428	350.935669
2021-10-29	439.450287	378.533234
2021-11-30	435.919373	386.091949
2021-12-31	457.231964	392.995117

265 rows × 2 columns

import matplotlib.pyplot as plt

# Set the plot size
plt.figure(figsize=(10, 5))

# Plot each line separately
plt.plot(ETFs_mensal.index, ETFs_mensal['SPY'], label='SPY')
plt.plot(ETFs_mensal.index, ETFs_mensal['QQQ'], label='QQQ')

# Set plot titles and labels
plt.title("SPY vs QQQ")
plt.xlabel("Date")
plt.ylabel("Preço ($)")

# Customize the y-axis to show dollar symbols
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'${x:,.0f}'))

# Add a legend
plt.legend()

# Show the plot
plt.show()

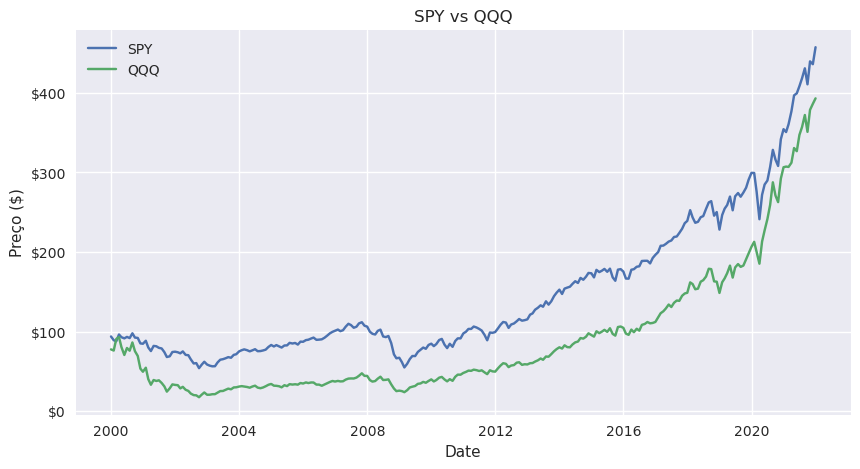
Aqui há o problema das duas séries temporais não começarem exactamente no mesmo ponto e por isso não conseguimos verdadeiramente comparar. Vamos fazer com que ambas comecem de 100:

# Fazer com que ambas as séries temporais comecem do mesmo ponto
ETFs_mensal = normalize(ETFs_mensal)

import matplotlib.pyplot as plt

# Set the plot size
plt.figure(figsize=(10, 5))

# Plot each line separately
plt.plot(ETFs_mensal.index, ETFs_mensal['SPY'], label='SPY')
plt.plot(ETFs_mensal.index, ETFs_mensal['QQQ'], label='QQQ')

# Set plot titles and labels
plt.title("SPY vs QQQ")
plt.xlabel("Date")
plt.ylabel("Preço ($)")

# Customize the y-axis to show dollar symbols
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'${x:,.0f}'))

# Add a legend
plt.legend()

# Show the plot
plt.show()

---

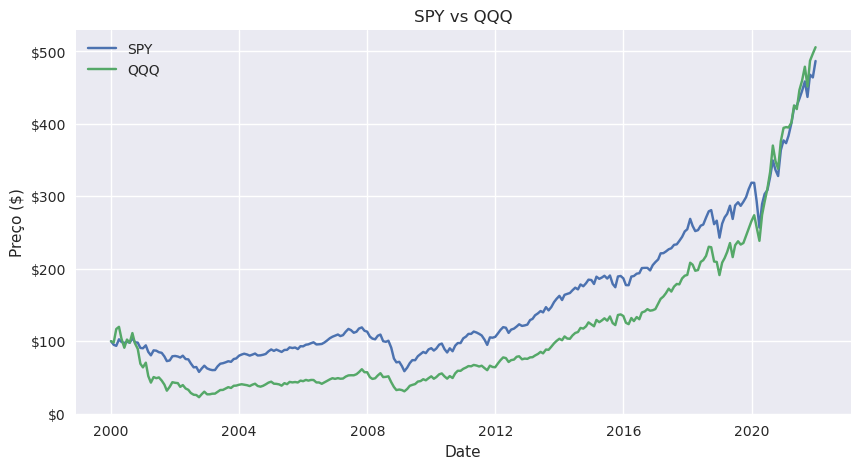
Gráfico de dispersão

Um gráfico de dispersão é um tipo de gráfico para visualizar a variação conjunta de duas variáveis. É uma ferramenta útil para exibir e entender possíveis relacionamentos entre as variáveis. É construído com o eixo do x a representar uma variável e o eixo do y representando a outra variável e usa pontos para indicar os valores das duas variáveis num determinado ponto no tempo.

Vamos continuar com o nosso exemplo do SPY e do QQQ. Para vermos a relação em duas séries temporais o que queremos comparar é os retornos.

ETFs_ret = ETFs_mensal.pct_change()
ETFs_ret

	SPY	QQQ
Date
1999-12-31	NaN	NaN
2000-01-31	-0.049787	-0.018468
2000-02-29	-0.015226	0.190244
2000-03-31	0.096915	0.025761
2000-04-28	-0.035120	-0.134703
...	...	...
2021-08-31	0.029760	0.042187
2021-09-30	-0.046605	-0.056832
2021-10-29	0.070164	0.078640
2021-11-30	-0.008035	0.019968
2021-12-31	0.048891	0.017880

265 rows × 2 columns

# Set the plot size
plt.figure(figsize=(10, 5))

# Create the scatter plot
sns.scatterplot(data=ETFs_ret, x='SPY', y='QQQ')

# Set plot titles and labels
plt.title("Scatter Plot of SPY vs QQQ")
plt.xlabel("SPY")
plt.ylabel("QQQ")

# Show the plot
plt.show()

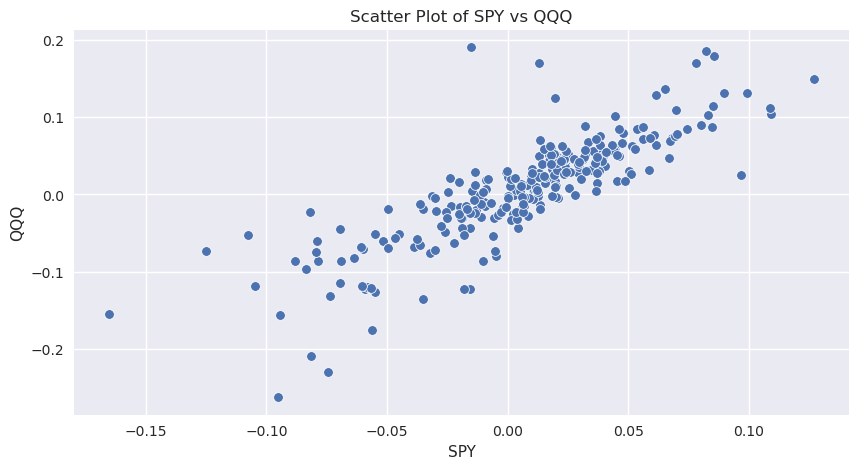
Fonte: https://www.latestquality.com/interpreting-a-scatter-plot/

Mapa de calor

Um mapa de calor é um tipo de gráfico que organiza e resume dados em uma tabela formato e os representa usando um espectro de cores. É ideal para gráficos de correlação. Ao SPY (ETF tracker do S&P 500) e ao QQQ (ETF tracker do Nasdaq) vamos juntar o DIA (ETF tracker do Dow Jones).

# Download das cotações
ETFs = download_yahoo_data(['SPY', 'QQQ', 'DIA'],
                            start='1999-12-31',
                            end='2021-12-31')

# Transformação em dados mensais
ETFs_mensal = ETFs.resample('BM').last()

# Calcular e usar retornos para comparações de correlação
ETFs_mensal_ret = ETFs_mensal.pct_change()

ETFs_mensal_ret

/tmp/ipykernel_158640/1178127103.py:7: FutureWarning: 'BM' is deprecated and will be removed in a future version, please use 'BME' instead.
  ETFs_mensal = ETFs.resample('BM').last()

	SPY	QQQ	DIA
Date
1999-12-31	NaN	NaN	NaN
2000-01-31	-0.049787	-0.018468	-0.048749
2000-02-29	-0.015226	0.190244	-0.071344
2000-03-31	0.096915	0.025761	0.079135
2000-04-28	-0.035120	-0.134703	-0.016718
...	...	...	...
2021-08-31	0.029760	0.042187	0.014479
2021-09-30	-0.046605	-0.056832	-0.042137
2021-10-29	0.070164	0.078640	0.059298
2021-11-30	-0.008035	0.019968	-0.035329
2021-12-31	0.048891	0.017880	0.057529

265 rows × 3 columns

# É sempre aconselhável tirar quaisquer na's
ETFs_mensal_ret = ETFs_mensal_ret.dropna()

ETFs_mensal_ret_corr = ETFs_mensal_ret.corr()

ETFs_mensal_ret_corr

	SPY	QQQ	DIA
SPY	1.000000	0.836279	0.954864
QQQ	0.836279	1.000000	0.734108
DIA	0.954864	0.734108	1.000000

import seaborn as sns

sns.heatmap(ETFs_mensal_ret_corr,
           annot=True,
           vmin=-1, vmax=1,
           cmap='coolwarm')

plt.show()

---

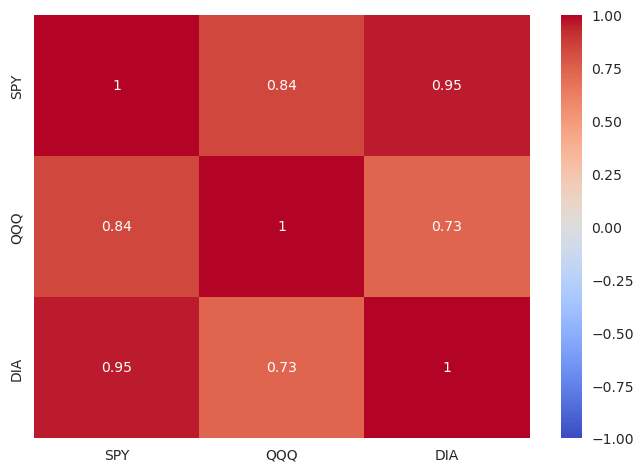
Medidas de Tendência Central

Uma medida de tendência central especifica onde os dados são centralizados. Alguns exemplos são a média (onde podemos encontrar vários tipos de médias), moda ou mediana.

Populações e amostras

Uma estatística é uma medida resumida de um conjunto de observações, e estatísticas descritivas resumem a tendência central e a variação de dispersão na distribuição de dados. Se a estatística resume o conjunto de todas as observações possíveis de uma população, referimo-nos estatística como um parâmetro. Se a estatística resume um conjunto de observações que é um subconjunto da população, referimo-nos à estatística como uma estatística de amostra, muitas vezes deixando de fora a palavra “amostra” e simplesmente referindo-se a ela como uma estatística. Enquanto as medidas de tendência central e localização pode ser calculado para populações e amostras, o nosso foco está em medidas de amostra (ou seja, estatísticas de amostra), pois é raro que um investimento o analista ou gestor esteja a lidar com uma população inteira de dados.

Média aritmética

A média aritmética é a soma dos valores das observações dividido pelo número de observações.

Exemplo de uma carteira com um terço em cada ETF

# Fazer um resample por ano 
ETFs_anual = ETFs.resample('BY').last()

# É recomendável que a cada passo vejam as alterações na DataFrame de forma 
# a verem se os passos fazem o que vocês pretendem

# Calcular retornos anuais
ETFs_anual_ret = ETFs_anual.pct_change()

# Apagar o primeiro ano para o qual nunca temos retorno
ETFs_anual_ret = ETFs_anual_ret.dropna()
ETFs_anual_ret_limpa = ETFs_anual_ret.copy()

# Calcular média aritmética de cada ano
# Seria o retorno de uma carteira com um terço em cada ETF.
# O \ é a forma de python saber que há uma quebra de linha
ETFs_anual_ret['Portfolio (1/3)'] = (ETFs_anual_ret['SPY'] + \
                                    ETFs_anual_ret['QQQ'] + \
                                    ETFs_anual_ret['DIA']) / 3

ETFs_anual_ret.head(10)

/tmp/ipykernel_158640/4112136288.py:2: FutureWarning: 'BY' is deprecated and will be removed in a future version, please use 'BYE' instead.
  ETFs_anual = ETFs.resample('BY').last()

	SPY	QQQ	DIA	Portfolio (1/3)
Date
2000-12-29	-0.097415	-0.361149	-0.060472	-0.173012
2001-12-31	-0.117585	-0.333447	-0.049726	-0.166919
2002-12-31	-0.215846	-0.373683	-0.146953	-0.245494
2003-12-31	0.281815	0.496685	0.279029	0.352510
2004-12-31	0.106980	0.105386	0.050227	0.087531
2005-12-30	0.048282	0.015654	0.016087	0.026675
2006-12-29	0.158453	0.071441	0.189142	0.139679
2007-12-31	0.051462	0.190280	0.087958	0.109900
2008-12-31	-0.367950	-0.417271	-0.321358	-0.368860
2009-12-31	0.263517	0.546841	0.227428	0.345929

Média ponderada

Mas nem sempre usamos a média aritmética. Neste caso podemos não ter uma carteira com o mesmo peso nos 3 ETFs. Devemos usar assim uma média ponderada, com o peso relativo respectivo de cada ETF na carteira.

# Média com diferentes pesos (40% SPY, 50% QQQ, 10% DIA) 
# Média com diferentes pesos (40% SPY, 50% QQQ, 10% DIA) 
# O \ é a forma de python saber que há uma quebra de linha
ETFs_anual_ret['Carteira (40/50/10)'] = ETFs_anual_ret['SPY'] * 0.4 + \
                                        ETFs_anual_ret['QQQ'] * 0.5 + \
                                        ETFs_anual_ret['DIA'] * 0.1

ETFs_anual_ret.head(10)

	SPY	QQQ	DIA	Portfolio (1/3)	Carteira (40/50/10)
Date
2000-12-29	-0.097415	-0.361149	-0.060472	-0.173012	-0.225588
2001-12-31	-0.117585	-0.333447	-0.049726	-0.166919	-0.218730
2002-12-31	-0.215846	-0.373683	-0.146953	-0.245494	-0.287875
2003-12-31	0.281815	0.496685	0.279029	0.352510	0.388972
2004-12-31	0.106980	0.105386	0.050227	0.087531	0.100507
2005-12-30	0.048282	0.015654	0.016087	0.026675	0.028749
2006-12-29	0.158453	0.071441	0.189142	0.139679	0.118016
2007-12-31	0.051462	0.190280	0.087958	0.109900	0.124521
2008-12-31	-0.367950	-0.417271	-0.321358	-0.368860	-0.387951
2009-12-31	0.263517	0.546841	0.227428	0.345929	0.401570

Média geométrica

Enquanto a média aritmética mostra-se ideal para calcular retornos ao longo de vários activos a média geométrica mostra-se ideal para calcular ao longo do tempo.

Médias aritméticas são boas para calcular ao longo de activos, médias geométricas ao longo do tempo.

Para calcular a rentabilidade anualizada do SPY não basta somar a rentabilidade de todos os anos e dividir pelo número de anos. Isto porque a rentabilidade do ano anterior é capitalizada à pela rentabilidade deste ano.

ETFs_anual.head(10)

	SPY	QQQ	DIA
Date
1999-12-31	93.924156	77.694092	67.138092
2000-12-29	84.774529	49.634926	63.078148
2001-12-31	74.806297	33.084293	59.941544
2002-12-31	58.659634	20.721258	51.132969
2003-12-31	75.190804	31.013205	65.400536
2004-12-31	83.234688	34.281548	68.685387
2005-12-30	87.253464	34.818203	69.790352
2006-12-29	101.079033	37.305645	82.990654
2007-12-31	106.280785	44.404175	90.290359
2008-12-31	67.174774	25.875580	61.274860

# Ver qual o valor de início
SPY_inicio = ETFs_anual['SPY'][0]
SPY_inicio

/tmp/ipykernel_158640/586412609.py:2: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  SPY_inicio = ETFs_anual['SPY'][0]

93.92415618896484

# Ver qual o valor de fim
SPY_fim = ETFs_anual['SPY'][-1]
SPY_fim

/tmp/ipykernel_158640/1505283722.py:2: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
  SPY_fim = ETFs_anual['SPY'][-1]

457.2319641113281

Recorrendo à fórmula de crescimento (calcular g) do capítulo anterior temos:

def compute_g(FV, PV, N):
    g = ((FV/PV)**(1/N))-1
    return g

g = compute_g(PV=SPY_inicio, FV=SPY_fim, N=21)

g

0.0782796136305326

Questão

O que é que o Valor de 0.783 representa?

Resolução

O SPY teve uma taxa de rentabilidade média anualizada de cerca de 7.83%. Esta é uma média geométrica e a taxa que sabendo o valor inicial e esta taxa conseguimos calcular o valor final.

Atenção que neste caso funcionou perfeitamente porque temos dados que começam e acabam no final de um ano e deu 21 anos. Podemos contudo calcular valores não inteiros de anos para sabermos g (por exemplo no caso do valor final ser durante o ano).

A média geométrica nunca poderá ser superior à média aritmética e quanto mais volátil a série temporal maior será a diferença entre ambas. Ou seja, na realidade quanto mais volátil o activo mais baixa a média geométrica face à aritmética. Se o activo, teoricamente, não tivesse volatilidade ambas as médias seriam iguais.

Função útil

from datetime import datetime
from dateutil.relativedelta import relativedelta
    
def compute_diference_in_years(start, end):
    start_date = pd.to_datetime(start)
    end_date = pd.to_datetime(end)
    difference  = end_date - start_date
    difference_in_years = (difference.days)/365.2421
    return difference_in_years

A função não dá exactamente 5 anos por questões de arredondamentos*.

• Na realidade é porque é complicado saber o número de dias no ano e usamos a melhor aproximação. Think you know how many days are in a year? Think again.

No caso da mediana quer dizer que 50% das rentabilidades anuais são superiores a 12.73% e metade são inferiores, independentemente de quanto superiores ou inferiores.

A mediana é um caso muito específico de quantil. Neste caso o 50%. Mas temos também a possibilidade de ter qualquer valor entre 0 e 100. Referimo-nos aos 25% como quartil, aos 20% como quintil, aos 10% como decil e 1% como percentil.

ETFs_anual_ret.describe()

	SPY	QQQ	DIA	Portfolio (1/3)	Carteira (40/50/10)
count	22.000000	22.000000	22.000000	22.000000	22.000000
mean	0.090392	0.116491	0.088638	0.098507	0.103266
std	0.178124	0.283448	0.152856	0.198588	0.222983
min	-0.367950	-0.417271	-0.321358	-0.368860	-0.387951
25%	0.013995	0.020430	0.004697	0.028973	0.029816
50%	0.127308	0.143255	0.096564	0.128953	0.121268
75%	0.208620	0.315528	0.205350	0.259481	0.278351
max	0.323078	0.546841	0.296414	0.352510	0.401570

QR ou diferença interquartil O IQR é a diferença entre o terceiro quartil (75%) e o primeiro quartil (25%). Nos diagramas de caixa é o rectângulo central preenchido.

Diagrama de caixa e gráficos de enxame

import seaborn as sns
import matplotlib.pyplot as plt

# Set the plot size
plt.figure(figsize=(10, 5))

# Create the box plot with all points displayed
sns.boxplot(data=ETFs_anual_ret, showmeans=True)
sns.stripplot(data=ETFs_anual_ret, color='black', alpha=0.5, jitter=True)  # Add points on the box plot

# Set plot titles and labels
plt.title("Box Plot of ETFs Annual Returns")
plt.xlabel("ETFs")
plt.ylabel("Returns")

# Show the plot
plt.show()

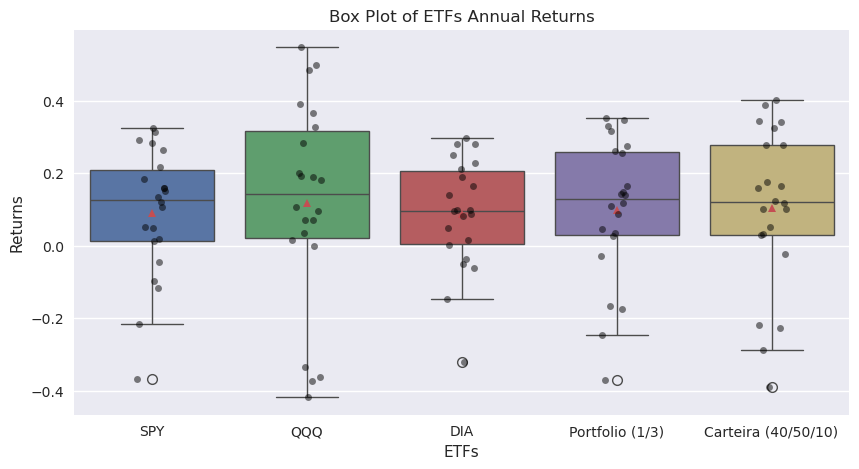
No gráfico podemos tanto ver os diagramas de caixa como os gráficos de enxame. Os gráficos de enxame mostram a rentabilidade de cada ano. Nos caso dos diagramas de caixa podemos ver os mesmos dados da função describe()

Exercício 2.5

Tendo em consideração o seguinte quadro:

Que compartimento de observações pertencem ao décimo percentil?

1. 2

2. 1 e 2

3. 19 e 20

O segundo quintil corresponde a que compartimento de observações?

1. 8

2. 5, 6, 7 e 8

3. 6, 7, 8, 9 e 10

O quarto quartil corresponde a que compartimento de observações?

1. 17

2. 17, 18, 19 e 20

3. 16, 17, 18, 19, 20

A mediana é mais próxima de:

1. 44.86

2. 46.88

3. 49.40

A amplitude de interquartil é mais próxima de:

1. 20.76

2. 23.62

3. 25.52

Resolução

1 - b) é o correcto porque o décimo percentil corresponde ao 10% de observações mais baixas da amostra, que são os compartimentos 1 e 2.

2 - b) é o correcto porque o segundo quintil corresponde às observações entre os percentis 20 e 40, ou seja aos compartimentos 5, 6, 7, e 8.

3 - c) é o correcto porque o último quartil corresponde aos últimos 25% de observações. Neste caso aos compartimentos 16, 17, 18, 19, 20

4 - b) é a solução correcta pois é exactamente o centro das observações. O limite superior do compartimento 10 é a fronteira entre os primeiros 50 percentis e os percentis 50 a 100.

5 - b) Se se lembram do diagrama de caixa o IQR inclui o primeiro, segundo e terceiro quartil. Ou seja para o calcular é o valor máximo do terceiro quartil menos o valor mínimo do segundo quartil. 58.34 - 34.72 = 23.62

---

Medidas de dispersão

A dispersão é a variabilidade em torno do centro da tendência. Se o retorno médio aborda a recompensa de determinado investimento, a dispersão aborda o risco. Nesta secção, iremos examinar as medidas mais comuns de dispersão: amplitude, desvio absoluto médio, variância e desvio padrão. Estas são todas medidas de dispersão absoluta. A dispersão absoluta é a quantidade de variabilidade presente sem comparação com qualquer ponto de referência ou benchmark.

Amplitude

O alcance é a diferença entre o máximo e valores mínimos em um conjunto de dados:

Dispersão = Valor máximo − Valor mínimo.

Pegando nos retornos mensais de SPY

SPY_mensal_ret.min()

SPY   -16.518677
dtype: float64

SPY_mensal_ret.max()

SPY    12.698323
dtype: float64

amplitude = SPY_mensal_ret.max() - SPY_mensal_ret.min()

amplitude

SPY    29.217001
dtype: float64

---

Desvio absoluto médio

As medidas de dispersão também podem ser calculadas usando todas as observações na distribuição em vez de apenas o mais alto e o mais baixo. Mas como devemos medir a dispersão? Poderíamos calcular medidas de dispersão como a média aritmética dos desvios em torno da média. Mas para que todos os desvios sejam positivos temos de calcular o valor absoluto desse valor.

Em português: MAD é a soma de um até n do valor absoluto (∣∣||∣∣) da observação menos a média. Tudo a dividir pelo número de observações.

Podemos usar uma fórmula com base na fórmula matemática:

Ou fazermos a nossa própria:

# Fazendo nós a fórmula
sum_abs_value = 0 # Criar uma valor para as somas

# Por cada valor em SPY_mensal_ret[''SPY']
for value in SPY_mensal_ret['SPY']: 
    # Somar o valor absoluto entre esse valor e a média
    sum_abs_value = sum_abs_value + abs(value - SPY_mensal_ret.mean().iloc[0])
    # Dividir as somas (sum_abs_value) pelo número de observações
    #  (len(SPY_mensal_ret['SPY'])
    mad = sum_abs_value/ len(SPY_mensal_ret['SPY']) 
    
mad

3.247015852140594

Transformando em fórmula:

def compute_mad(data):
    # Data deve ser um numpy array ou pandas series (não dataframe)
    sum_abs_value = 0 # Criar uma valor para as somas
    
    for value in data: # Por cada valor em data
        # Somar o valor absoluto entre esse valor e a média
        sum_abs_value = sum_abs_value + abs(value - data.mean())
        # Dividir as somas (sum_abs_value) pelo número de observações (len(data))
        mad = sum_abs_value/ len(data) 
    return mad
    
mad = compute_mad(SPY_mensal_ret['SPY'])
mad

3.247015852140594

O MAD é uma percentagem, por isso podem multiplicar por 100:

mad * 100

324.7015852140594

---

Variância e desvio padrão de uma amostra

O desvio absoluto médio abordou a questão de valores de desvios serem negativos através do uso do valor absoluto dos desvios. Uma segunda abordagem ao tratamento dos desvios é eleva-los ao quadrado. A variância e o desvio padrão, que se baseiam no quadrado dos desvios, são as duas medidas de dispersão mais usadas. A variância é definida como a média dos desvios quadrados em torno da média. O desvio padrão é a raiz quadrada positiva da variância. A seguir abordamos o cálculo e uso de variância e desvio padrão.

Variância de uma amostra

Em português: Variância da amostra é a soma de um até n do quadrado (²​​) das observações menos a média. Tudo a dividir pelo número de observações - 1.

Porquê -1?

Usamos n se for a população total e n-1 se for uma amostra. O n-1 chama-se Correcção de Bessel.

“Em estatística , a correcção de Bessel é o uso de n - 1 em vez de n na fórmula para a variância da amostra e o desvio padrão da amostra , onde n é o número de observações em uma amostra . Este método corrige o enviesamento na estimativa da variância da população. Também corrige parcialmente o enviesamento na estimativa do desvio padrão da população..”

Podemos usar uma fórmula pré-feita do pandas:

SPY_mensal_ret['SPY'].var()

18.79683247580178

var_top_value = 0 # Criar uma valor para as somas

for value in SPY_mensal_ret['SPY']: # Por cada valor em SPY_mensal_ret['SPY']
    # Somas do quadrado (**2) de cada valor - a média
    var_top_value = var_top_value + (value - SPY_mensal_ret.mean().iloc[0]) ** 2 
    # Dividir as somas (var_top_value) pelo número de observações - 1 
    # (len(SPY_mensal_ret['SPY'])
    var = var_top_value/ (len(SPY_mensal_ret['SPY'])-1) 
    
var

18.79683247580178

Desvio padrão de uma amostra

Como a variância é medida em unidades quadradas, precisamos de uma maneira de retornar ao unidades originais. Podemos resolver este problema usando o desvio padrão, a raiz quadrada da variância. O desvio padrão é mais facilmente interpretado do que a variância porque o desvio padrão é expresso na mesma unidade de medida das observações.

Podemos usar uma fórmula pré-feita do pandas:

SPY_mensal_ret['SPY'].std(ddof=1)
# ddof é muito importante

4.33553139485828

Calcular o desvio padrão como a raiz quadrada da variância

stdev = var**(1/2)

stdev

4.33553139485828

Com base nesse conhecimento podemos fazer a nossa função de desvio padrão derivada da função de variância:

---

Semi-variância e coeficiente de variação

A variância ou desvio padrão dos retornos de um activo é frequentemente interpretado como uma medida do risco de um activo. A variação e o desvio padrão dos retornos levam em consideração os retornos acima e abaixo da média. No entanto, os investidores normalmente preocupam-se apenas com o risco de queda, retornos abaixo da média ou abaixo de algum retorno mínimo especificado. Como resultado, os analistas desenvolveram medidas de risco de desvalorização ou subida menor que o esperado.

Semi-variância

Na prática, podemos estar preocupados com valores de retorno (ou outra variável) abaixo algum nível diferente da média. Por exemplo, se nosso objectivo de retorno for de 6,0% ao ano (nosso retorno mínimo aceitável), então podemos estar preocupados particularmente com retornos abaixo de 6,0% ao ano. Os 6,0% é a meta. O semi-desvio alvo, é uma medida de dispersão das observações (aqui, retornos) abaixo do alvo. Para calcular um semi-desvio alvo de amostra, primeiro especificamos o nosso objectivo mínimo.

Fórmula:

passando a fórmula para python:

def compute_target_downside_deviation(dataseries, target):
    sum_values = 0 # Criar uma valor para as somas
    
    for value in dataseries: # Por cada valor na dataframe
        if value  < target:
            sum_values = sum_values + ((value - target) ** 2)
    
    sum_values_division = sum_values / (len(dataseries) - 1)
 
    return np.sqrt(sum_values_division)

Exercício 2.6

Um portefólio teve retornos mensais de: 5, 3, -1, -4, 4, 2, 0, 4, 3, 0, 6 e 5 para cada mês de um determinado ano.

1. Calcule o semi-desvio alvo quando o alvo é 3%.

2. Se o alvo fosse 4% a sua resposta seria diferente? Sem usar quaisquer cálculos explique.

Resolução

retornos = np.array([5, 3, -1, -4, 4, 2, 0, 4, 3, 0, 6, 5])

compute_target_downside_deviation(retornos, target=3)

2.76339711883103

compute_target_downside_deviation(retornos, target=4)

3.3978602892783196

Se o retorno alvo for maior, então os desvios abaixo do objectivo serão maiores para além de existirem mais valores nos desvios e desvios quadrados abaixo do alvo; assim, a semi-desvio alvo seria maior.

O downside deviation é na maioria das vezes menor que o desvio padrão, pois exclui variações acima do target. O objectivo é medirmos o portfolio com vista apenas nas quedas (caso o objectivo seja 0) ou quando o retorno é abaixo de um objectivo (ou até da média). O facto de ser mais baixo acaba por nos informar que do ponto de vista do investidor o desvio padrão muitas vezes sobrevaloriza o risco, ao incluir volatilidade positiva.

Coeficiente de variação

O coeficiente de variação é uma medida de dispersão relativa. Devido a ser um rácio faz com que possamos comparar investimentos que são bastante diferentes. Como o rácio tem em consideração não só o desvio padrão mas também a média, significa que um investimento com maior desvio padrão poderá ter um melhor coeficiente de variação (mais baixo) se a média aumentar ainda mais em termos relativos (exemplo em baixo).

O coeficiente de variação igual a desvio padrão a dividir pela média.

def compute_cv(dataseries, ddof=1):
    cv = dataseries.std(ddof=ddof) / dataseries.mean()
    return cv

cv = compute_cv(retornos)

cv

1.314684396244359

---

Exercício 2.7

1. Calcule a média aritmética dos retornos de cada indústria

2. Calcule o desvio padrão dos retornos de cada indústria

3. Calcule o coeficiente de variação dos retornos de cada indústria

Resolução

import pandas as pd

# Corrected data
dados_listas = {
    'Empresa': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    'Industria A': [-5, -3, -1, 2, 4, 6, 7, 9, 10, 11],
    'Industria B': [-10, -9, -7, -3, 1, 3, 5, 18, 20, 22],
    'Industria C': [7, 12, -7, -3, 5, 3, 5, -20, 30, 50]
}

# Create DataFrame
dados = pd.DataFrame(dados_listas)

dados

	Empresa	Industria A	Industria B	Industria C
0	1	-5	-10	7
1	2	-3	-9	12
2	3	-1	-7	-7
3	4	2	-3	-3
4	5	4	1	5
5	6	6	3	3
6	7	7	5	5
7	8	9	18	-20
8	9	10	20	30
9	10	11	22	50

1. Calcular a média aritmética dos retornos de cada indústria

dados['Industria A'].mean()

4.0

dados['Industria B'].mean()

4.0

dados['Industria C'].mean()

8.2

2. Calcular o desvio padrão dos retornos de cada indústria

dados['Industria A'].std(ddof=1)

5.597618541248888

dados['Industria B'].std(ddof=1)

12.119772641798562

dados['Industria C'].std(ddof=1)

19.543683264818725

3. Calcular o coeficiente de variação dos retornos de cada indústria

compute_cv(dados['Industria A'])

1.399404635312222

compute_cv(dados['Industria B'])

3.0299431604496405

compute_cv(dados['Industria C'])

2.383376007904723

A forma das distribuições

Assimetria de uma distribuição

Uma característica importante de interesse para os analistas é o grau de simetria nas distribuições de retorno.

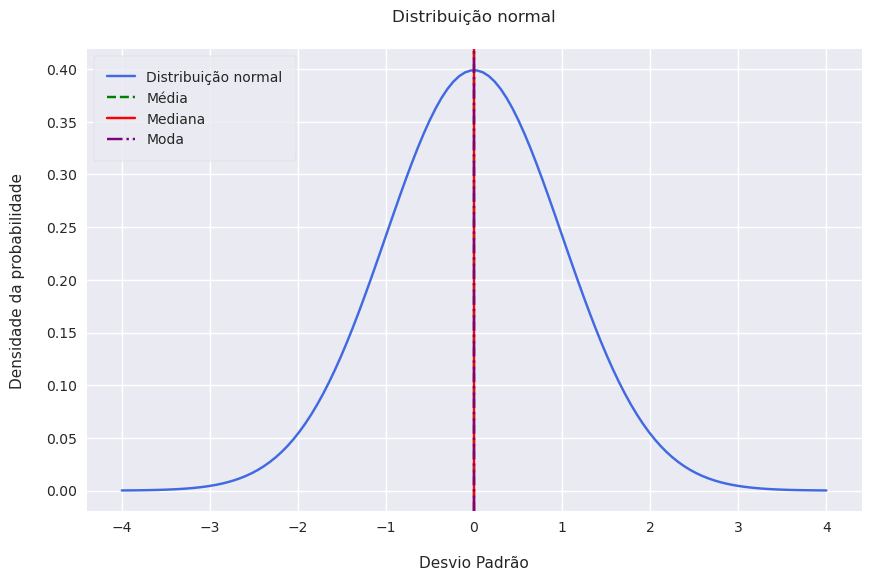
Se uma distribuição de retorno é simétrica em relação à sua média, cada lado da distribuição é uma imagem espelhada do outro. Assim, intervalos iguais de perda e ganho exibem a mesma frequências. Se a média for zero, por exemplo, então perdas de -5% a -3% ocorrem com aproximadamente a mesma frequência que os ganhos de 3% a 5%. Esse é o caso de uma distribuição normal.

Show code cell source Hide code cell source

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Set the mean and standard deviation of the normal distribution
mean = 0
std_dev = 1

# Generate points on the x axis
x_values = np.linspace(-4, 4, 120)

# Calculate the normal distribution's probability density function (PDF)
y_values = (1 / (std_dev * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x_values - mean) / std_dev) ** 2)

# Set the style to 'darkgrid'
sns.set_style('darkgrid')

# Adjusting the figure size
plt.figure(figsize=(10, 6))

# Plot the normal distribution with a 'royalblue' line
plt.plot(x_values, y_values, label='Distribuição normal', color='royalblue')

# Since the normal distribution is symmetric, mean = median = mode
# Plot lines for mean, median, and mode
plt.axvline(x=mean, color='green', linestyle='--', label='Média')
plt.axvline(x=mean, color='red', linestyle='-', label='Mediana')
plt.axvline(x=mean, color='purple', linestyle='-.', label='Moda')

# Add title and labels with the requested titles in Portuguese
plt.title('Distribuição normal', pad=20)
plt.xlabel('Desvio Padrão', labelpad=15)
plt.ylabel('Densidade da probabilidade', labelpad=15)

# Show the legend with a frame and increase the padding
plt.legend(frameon=True, loc='upper left', borderpad=1)

# Display the plot
plt.show()

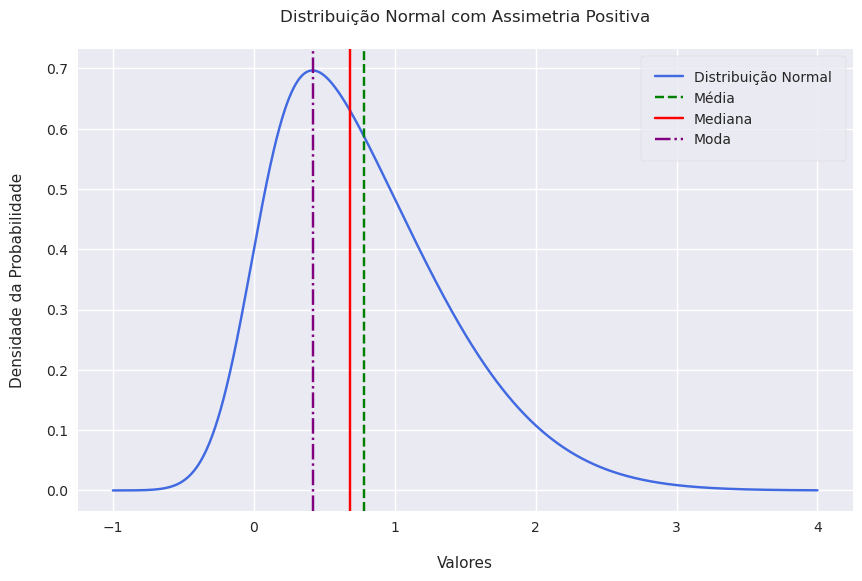
Show code cell source Hide code cell source

from scipy.stats import skewnorm

# Parameters for the skewed normal distribution
a = 4  # Positive value for positive skewness
mean = 0
std_dev = 1

# Create a skewed normal distribution object
skewed_distribution = skewnorm(a, mean, std_dev)

# Generate points on the x axis
x_values = np.linspace(-1, 4, 1000)

# Calculate the PDF of the skewed normal distribution
y_values = skewed_distribution.pdf(x_values)

# Calculate mean, median, mode
# For a skewed normal distribution, these are not as straightforward to calculate,
# so we'll sample from the distribution
samples = skewed_distribution.rvs(10000)
sample_mean = np.mean(samples)
sample_median = np.median(samples)
sample_mode = 0.42

# Plot the skewed normal distribution
plt.figure(figsize=(10, 6))
sns.set_style('darkgrid')
plt.plot(x_values, y_values, label='Distribuição Normal', color='royalblue')

# Plot lines for mean, median, and mode
plt.axvline(x=sample_mean, color='green', linestyle='--', label='Média')
plt.axvline(x=sample_median, color='red', linestyle='-', label='Mediana')
plt.axvline(x=sample_mode, color='purple', linestyle='-.', label='Moda')

# Add labels and a legend
plt.title('Distribuição Normal com Assimetria Positiva', pad=20)
plt.xlabel('Valores', labelpad=15)
plt.ylabel('Densidade da Probabilidade', labelpad=15)
plt.legend(frameon=True, loc='upper right', borderpad=1)

# Show the plot
plt.show()

Show code cell source Hide code cell source

from scipy.stats import skewnorm

# Parameters for the skewed normal distribution
a = -3  # Positive value for positve skewness
mean = 0
std_dev = 1

# Create a skewed normal distribution object
skewed_distribution = skewnorm(a, mean, std_dev)

# Generate points on the x axis
x_values = np.linspace(1, -4, 1000)

# Calculate the PDF of the skewed normal distribution
y_values = skewed_distribution.pdf(x_values)

# Calculate mean, median, mode
# For a skewed normal distribution, these are not as straightforward to calculate,
# so we'll sample from the distribution
samples = skewed_distribution.rvs(10000)
sample_mean = np.mean(samples)
sample_median = np.median(samples)
sample_mode = -0.47

# Plot the skewed normal distribution
plt.figure(figsize=(10, 6))
sns.set_style('darkgrid')
plt.plot(x_values, y_values, label='Distribuição Normal', color='royalblue')

# Plot lines for mean, median, and mode
plt.axvline(x=sample_mean, color='green', linestyle='--', label='Média')
plt.axvline(x=sample_median, color='red', linestyle='-', label='Mediana')
plt.axvline(x=sample_mode, color='purple', linestyle='-.', label='Moda')

# Add labels and a legend
plt.title('Distribuição Normal com Assimetria Negativa', pad=20)
plt.xlabel('Valores', labelpad=15)
plt.ylabel('Densidade da Probabilidade', labelpad=15)
plt.legend(frameon=True, loc='upper right', borderpad=1)

# Show the plot
plt.show()

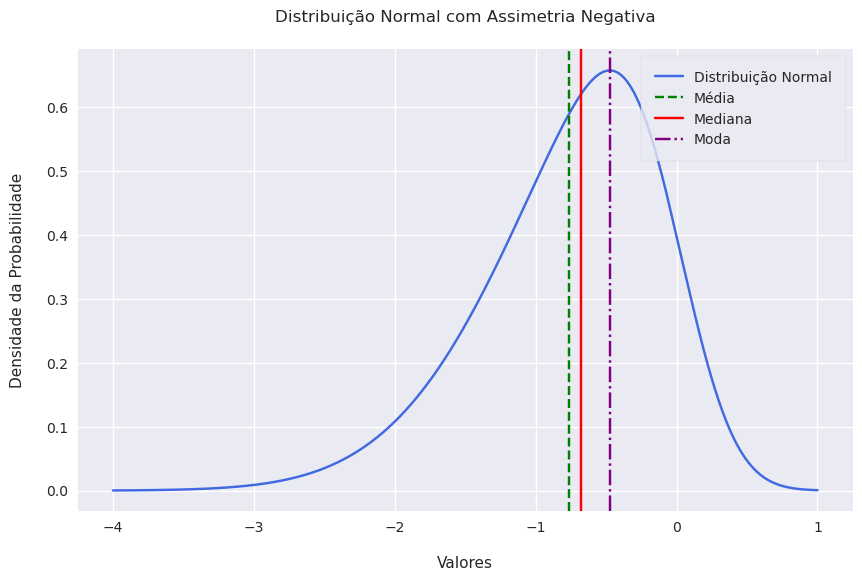
O formato da distribuição: Curtose

Na secção anterior, discutimos como determinar se uma distribuição de retorno se desvia de uma distribuição normal devido à assimetria. Outra forma de em que distribuição de retorno pode diferir de uma distribuição normal é sua tendência relativa para gerar grandes desvios da média. A maioria dos investidores entende uma maior probabilidade de desvios extremamente grandes da média como risco crescente. A curtose é uma medida do peso combinado das caudas de uma distribuição relativamente ao para o resto da distribuição - isto é, a proporção da probabilidade total que é fora de, digamos, 2,5 desvios padrão da média. Uma distribuição que tem caudas mais gordas do que a distribuição normal é referida como leptocúrtica ou cauda gorda; uma distribuição que tem caudas mais finas do que a distribuição normal é referida como sendo platicúrtica ou cauda fina; e uma distribuição semelhante à distribuição normal no que diz respeito peso nas caudas é chamada de mesocúrtica. Uma distribuição de cauda gorda (cauda fina) tende a para gerar desvios extremamente grandes mais frequentes (menos frequentes) da média que a distribuição normal.

# Lisa de retornos do SPY para testar contra a distribuição normal
spy_returns_array = SPY['SPY'].pct_change().dropna().values * 100

# Calcular uma distribuição normal
normal = np.random.normal(size=1_000_000)

KDE plot dos retornos do SPY vs distribuição normal

Show code cell source Hide code cell source

plt.rcParams["figure.figsize"] = (15,6)

fig, ax = plt.subplots()

sns.kdeplot(spy_returns_array, ax=ax, label='Distribuição retornos do SPY')
sns.kdeplot(normal, ax=ax, linestyle="--",
                    color='grey', label='Distribuição normal')
plt.ylabel('Densidade da probabilidade', fontsize=14)
plt.yticks(fontsize= 12)
plt.xlabel('Desvio Padrão', fontsize=14)
plt.xticks(fontsize= 12)
plt.legend()
plt.xlim([-3.5, 3.5]);
plt.show()

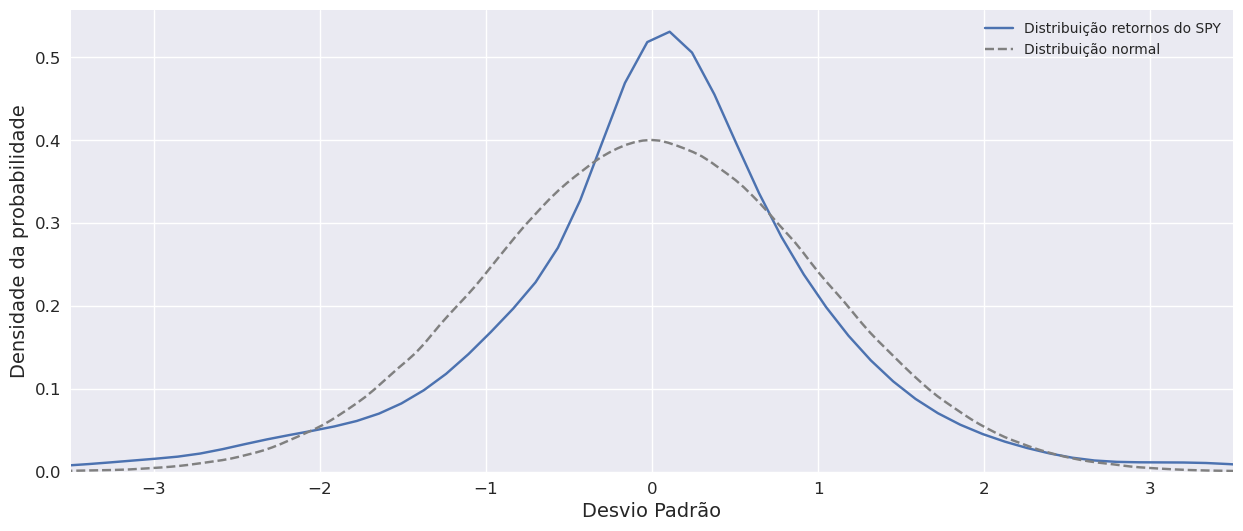
Daí se dizer que os mercados são fat-tailed e/ou têm caudas gordas (linha azul mais alta que a cinza nas pontas logo maior probabilidade de haver movimentos extremos).

Curtose do SPY

import scipy.stats as stats

round(stats.kurtosis(spy_returns_array),2)

12.35

Curtose da distribuição normal

# Neste caso apenas aroximadamente zero porque estamos a fazer uma normal de um sample de 1 milhão de pontos!
round(stats.kurtosis(normal),2)

0.01

Como podemos ver os retornos do SPY têm caudas pesadas, o que a torna numa distribuição leptocúrtica, em que a curtose é superior a 3. Uma vez que a distribuição normal acaba por ser a distribuição padrão dentro deste estilo muita vezes só se fala em “kurtosis em excesso”. Muito importante num software sabermos se o que está a ser calculado é a kurtosis ou a curtose em excesso (pode ser diferente em cada software).

Correlação entre duas variáveis

A correlação é uma medida da relação linear entre duas variáveis aleatórias. O primeiro passo é considerar como duas variáveis variam juntas é a a sua covariância.

Dito de forma simples, a covariância é uma medida da variabilidade conjunta de duas variáveis aleatórias. Se as variáveis aleatórias variam na mesma direcção - por exemplo, X tende a ser acima de sua média quando Y está acima de sua média, e X tende a estar abaixo de sua média quando Y está abaixo da sua média, então a sua covariância é positiva. Se as variáveis variam no sentido oposto relativamente às suas respectivas médias, então sua covariância é negativa.

Por si só, o tamanho da medida de covariância é difícil de interpretar, pois não é normalizado e, portanto, depende da magnitude das variáveis. Isso leva-nos à versão normalizada da covariância, que é o coeficiente de correlação.

A correlação da amostra é uma medida padronizada de como duas variáveis se movem em conjunto. O coeficiente de correlação da amostra (rXY) é a razão da covariância da amostra para o produto dos desvios padrão das duas variáveis:

É importante dizer que o coeficiente de correlação expressa a força da relação linear entre as duas variáveis aleatórias.

Discutimos agora o coeficiente de correlação, ou simplesmente correlação, e suas propriedades mais detalhadamente:

1. A correlação varia de -1 e +1 para duas variáveis aleatórias, X e Y: −1 ≤ rXY ≤ +1.

2. Uma correlação de 0 (variáveis não correlacionadas) indica a ausência de qualquer (ou seja, em linha recta) entre as variáveis.

3. Uma correlação positiva próxima de +1 indica uma forte relação linear positiva. Uma correlação de 1 indica uma relação linear perfeita.

4. Uma correlação negativa próxima de -1 indica um forte negativo (ou seja, inverso) relação linear. Uma correlação de -1 indica uma linearidade inversa perfeita relação.

Problemas com a correlação

=> Não é ideal para as já referidas relações não lineares;

=> Susceptível a outliers;

=> “Correlação não implica causalidade” (“Academics David Leinweber and David Krider drove this point home by showing that there was a very high 87% correlation between the annual level of the S&P 500 and the annual production of butter in Bangladesh.”)