Capítulo 5 - Amostras e estimação

Capítulo 5 - Amostras e estimação#

1 - Introdução#

Todos os dias vemos a variação em índices bolsistas como o S&P 500, o Nikkei 225 ou o Eurostoxx 50 e os consideramos como representativos dos mercados bolsistas das respectivas regiões. Embora o S&P 500, o Nikkei ou Eurostoxx não representem as populações de acções americanas ou japonesas, vemos esses como indices como indicadores válidos de todo o comportamento da população.

Como analistas, estamos acostumados a usar essas informações de amostra para avaliar o desempenho de vários mercados de todo o mundo. Qualquer estatística que calculemos com informações de amostra, no entanto, são apenas estimativas dos parâmetros populacionais subjacentes. Uma amostra, então, é um subconjunto da população – um subconjunto estudado para inferir conclusões sobre a própria população.

Neste capítulo vamos discutimos a o processo de obtenção de uma amostra.

2 - O processo de obtenção de uma amostra#

A informação sobre uma população que tentamos obter geralmente diz respeito ao valor de um parâmetro, uma quantidade calculada ou usada para descrever uma população de dados. Quando usamos uma amostra para estimar um parâmetro, fazemos uso de estatísticas amostrais (ou simplesmente estatísticas). Uma estatística é uma quantidade calculada ou usada para descrever uma amostra de dados.

2.1 - Amostras aleatórias simples#

Quando escolhemos usar uma amostra, devemos formular um plano para a obtenção dessa amostra.

Qualquer tipo de amostra introduz erro. O erro surge porque nem todas a é ou pode ser usada. Entramos assim num campo de decidir entre tempo e dinheiro e a qualidade e tamanho da amostra.

Mas como seleccionar a amostra?

O tipo básico de amostra de que podemos tirar conclusões estatisticamente sólidas sobre uma população é a amostra aleatória simples (amostra aleatória, para abreviar).

Amostra Aleatória Simples - Uma amostra aleatória simples é um subconjunto de uma população maior criada de tal forma que cada elemento da população tem uma probabilidade igual de ser seleccionado para o subconjunto.

A amostra aleatória simples é particularmente útil quando os dados da população são homogéneos

isto é, as características do dados ou observações (por exemplo, tamanho ou região) são amplamente semelhantes. Veremos que se isso condição não for satisfeita, outros tipos de formas de obtenção de amostras podem ser mais apropriadas.

As estatísticas obtidas através da amostra serão diferentes do parâmetros da população que estamos a tentar estimar. Está sujeito a erro. Uma parte importante deste O erro é conhecido como erro da amostra, que vem da variação da amostra e ocorre porque temos dados sobre apenas um subconjunto da população.

Uma amostra aleatória deverá reflectir as propriedades da população de forma imparcial, e as estatísticas amostrais, como a média ou o desvio padrão calculada com base numa amostra deverão ser estimativas válidas dos parâmetros populacionais subjacentes.

Erro da amostra - O erro de amostra é a diferença entre o valor observado de uma estatística e a quantidade que se pretende estimar. É o resultado do uso de subconjuntos da população.

2.2 - Amostra aleatória estratificada#

O método de amostragem aleatória simples que acabamos de discutir pode não ser a melhor abordagem em todas as situações. Uma alternativa frequentemente utilizada é a amostra aleatória estratificada.

Amostra aleatória estratificada - Na amostra aleatória estratificada a população é dividida em subpopulações (estratos) com base num ou mais critérios de classificação. Amostras aleatórias simples são então retiradas de cada estrato em tamanhos proporcionais ao tamanho relativo de cada estrato na população. Essas amostras são então agrupadas para formar uma amostra aleatória estratificada.

Em contraste com a amostragem aleatória simples, a amostragem aleatória estratificada garante que as subdivisões populacionais de interesse estejam representadas na amostra. Outra vantagem é que as estimativas de parâmetros produzidos a partir de amostragem estratificada têm maior precisão - isto é, menor variância ou dispersão - do que as estimativas obtidas por amostragem aleatória simples.

Na área de investimentos a amostra aleatória estratificada é usada em fundos e ETFs trackers de índices obrigacionistas. Como muitas vezes é impossível (devido a problemas de liquidez) ou impraticável (devido a determinados índices terem milhares de obrigações) comprar todas as obrigações do índice o gestor segue este tipo de amostra pois representa melhor o índice do que seleccionar aleatoriamente obrigações. Ele divide as obrigações por diferentes estratos tendo em consideração as características de diferentes obrigações e consegue assim, de uma forma mais eficiente, imitar o índice (que neste caso é a população).

3 - A distribuição da média da amostra e o teorema do limite central#

Supondo que a amostra é representativa da população, como podemos avaliar o erro da amostra na estimativa da população? A média amostral é ela própria uma variável aleatória com uma distribuição de probabilidade. Para estimar se podemos esperar que a média da amostra corresponda à média da população subjacente precisamos entender a distribuição amostral da média. Felizmente o teorema do limite central, que nos ajuda a entender a amostra da distribuição da média para muitos dos problemas de estimação que enfrentamos.

3.1 - Teorema do limite central#

O teorema do limite central diz-nos que quando o tamanho da amostra aumenta, a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal.

O que é que isso quer dizer na realidade? Vamos assumir que estamos queremos fazer uma amostra aleatória simples. Se todos os elementos da população têm a mesma probabilidade de serem escolhidos isso não dá origem a uma distribuição normal mas sim a uma uniforme.

Resumindo, de acordo com o teorema do limite central, quando a amostra de qualquer distribuição, a distribuição da média das amostras terá sempre as seguintes propriedades desde que a quantidade de amostras seja suficientemente grande.

A distribuição da média das amostras \(\overline{X}\) será aproximadamente normal;
A média da distribuição de \(\overline{X}\) será idêntica a à média da população de onde as amostras são retiradas;
A variância da distribuição de \(\overline{X}\) será idêntica a à média da população de onde as amostras são retiradas;

Desta forma, o teorema do limite central permite-nos fazer declarações de probabilidade bastante precisas sobre a média populacional usando a média amostral, qualquer que seja a distribuição da população.

3.2 - Erro padrão da média#

O teorema do limite central afirma que a variância da distribuição da média amostral é \(\frac {\sigma^2}{n}\) . O desvio padrão de uma estatística amostral é conhecido como erro padrão da estatística. O erro padrão da média amostral é uma de grande importância na aplicação do teorema do limite central na prática.

Erro padrão da média - Para a média da amostra \(\overline{X}\) calculado a partir de uma amostra gerada por uma população com desvio padrão σ,

o erro padrão da média amostral é dado por uma das duas expressões:

\(\sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}}\)

se soubermos \(\sigma\), o desvio padrão da população, ou:

\(s_{\overline{X}} = \frac{s}{\sqrt{n}}\)

quando não sabemos o desvio padrão da população e precisamos de usar o desvio padrão da amostra.

\(\sigma\) é o desvio padrão da população, \(s\) o desvio padrão da amostra e \(n\) o tamanho da amostra.

Na prática vamos quase sempre usar a segunda fórmula. A estimativa de s pode ser calculada através de:

\(s^2 = \frac{\sum_{i=1}^{n} (X_i-\overline{X})^2}{n-1}\)

Vale a pena dizer que embora o erro padrão seja o desvio padrão da distribuição amostral do parâmetro, “desvio padrão” em geral e “erro padrão” são dois conceitos distintos, e os termos não são intercambiáveis. Simplificando, o desvio padrão mede a dispersão dos dados da média, enquanto o erro padrão mede a imprecisão de uma estimativa de parâmetro populacional (devido a ser uma amostra).

4 - Estimativas da média da população#

As fórmulas que usamos para calcular a média amostral e todas as outras estatísticas amostrais são exemplos de estimadores.A estimação da média da amostral pode e produzirá resultados diferentes em diferentes amostras mesmo que sejam da mesma população.

Muitas vezes, temos uma escolha entre vários estimadores possíveis. Aquele que devemos seleccionar deverá ter três características: imparcialidade (falta de enviesamento), eficiência e consistência.

Definições

Imparcialidade: - Um estimador imparcial é aquele cujo valor esperado (a média de sua distribuição amostral) é igual ao parâmetro que se pretende estimar.
Eficiência: Um estimador imparcial é eficiente se nenhum outro estimador imparcial do mesmo parâmetro tem uma distribuição amostral com menor variância.
Consistência: Um estimador consistente é aquele para o qual a probabilidade de estimativas próximas ao valor do parâmetro populacional aumenta à medida que o tamanho da amostra aumenta.

Exercício

Distribuições amostrais de um estimador

O gráfico em cima tem três distribuições amostrais, com diferentes n, da média da população. A linha vertical a tracejado mostra o valor real da média da população.

Qual das seguintes frases melhor descreve as propriedades do estimador?

A. O estimador é imparcial;

B. O estimador é enviesado e inconsistente;

C. O estimador é enviesado mas consistente.

Resolução

5 - Intervalos de confiança para a média da população#

Quando precisamos de um único número como estimativa de um parâmetro populacional, fazemos uso de uma estimativa pontual. No entanto, devido ao erro de amostragem, a estimativa pontual não é probabilidade de igualar o parâmetro populacional em qualquer amostra. Frequentemente, uma ferramenta mais útil é encontrar um intervalo de valores que esperamos entre o parâmetro com um nível especificado de probabilidade - uma estimativa de intervalo de o parâmetro. Um intervalo de confiança cumpre esse papel.

Definição

Intervalo de confiança - Intervalo de confiança é um intervalo para o qual se pode afirmar com uma dada probabilidade 1 − \(α\), chamada grau de confiança, que esse intervalo conterá o parâmetro que se pretende estimar. Este intervalo é muitas vezes referido como intervalo de confiança de para o parâmetro.

5.1 - Construção de intervalos de confiança#

Exemplo de um intervalo de confiança com base numa distribuição normal:

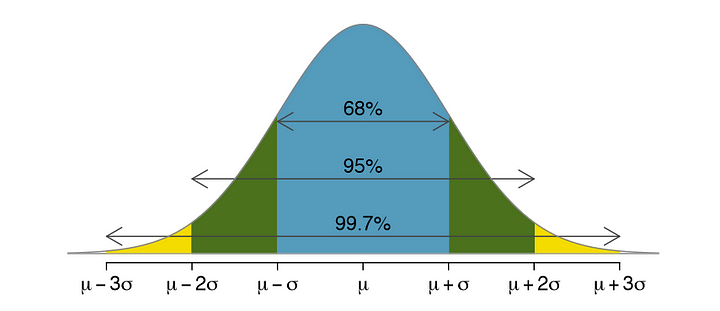
μ é a média da população
σ é o desvio padrão

Isto foi o caso de um intervalo de confiança baseado numa distribuição normal.

Quando é que podemos usar a distribuição normal?

Intervalos de confiança para a média de população, sendo que esta é normalmente distribuida e variança conhecida;
Intervalos para a média da população com variancia desconhecida mas quando a amostra é grande (>30 normalmente);

Como vimos no exercício 5.03 acima mesmo que não tenhamos a certeza da distribuição da população podemos construir um intervalo para a média da população se a amostra é grande, recorrendo ao Teorema do Limite Central.

O que fazer quando a distribuição é desconhecida MAS a amostra é pequena?

Devemos usar a distribuição T de Student.

A distribuição T de Student é uma distribuição simétrica (como a normal) e definida apenas por um parâmetro, os Graus de liberdade.

Quanto maior os graus de liberdade mais próximo de uma distribuição Normal fica.

6- Enviesamentos#

6.1 - Data Mining Bias#

O enviesamento de Data Mining refere-se ao abuso dos dados que temos para análise. Ou seja, muitas vezes focamo-nos na pesquisa de relações onde não existem necessariamente mas estão presentes nos dados. Um foco demasiado grande nos dados pode acabar por nos dizer que existe uma relação quando na realidade não existe.

Um caso no mundo financeiro é o uso de trading e estratégias que funcionaram no passado, levando muitas vezes a uma grande alegria inicial de quem as desenvolveu para depois ver que em tempo real (depois do período testado) não funcionarem.

Há até um ditado “Se torturares suficientemente os dados eles vão acabar por confessar”. Uma alusão a que muitas vezes conseguimos quase tudo o que quisermos dos dados e obter “resultados” com base no passado mas sem qualquer validade futura.

Ou seja:

Quando há demasiada minuciosidade no tratamento dos dados: Uma estratégia de trading que compre todas as segundas terças feiras do mês e venda na última Quinta feira do mês;

Quando não há um racional por trás: Voltamos às correlações espúrias como a produção de manteiga do Bangladesh ter uma correlação alta com a perormance do S&P que já vimos num capítulo anterior*.

O ser humano muitas vezes também gosta demasiado de histórias, portanto também há o reverso da medalha. Precisamos de dados para suportar conclusões e “histórias” que muitas vezes parecem fazer sentido. Precisamos de um equilíbrio entre os dois.

6.2 - Sample selection Bias#

O enviesamento de selecção de amostra pode ser visto, no que diz respeito ao mercado financeiro, no survivorship bias. O enviesamento de sobrevivência vem do facto de nós por exemplo usarmos, para análise, os fundos de investimento existentes neste momento para uma análise do passado.

Fundos de investimento são fechados ou fundidos quando não têm boas performances. Naturalmente os que sobreviveram são os que tiveram melhores performances. Se só tivermos em considerção os fundos que sobreviveram estamos a sobrevalorizar a performance que teriamos se tivessemos investido em 1980. Por exemplo um mercado que é muito analisado é o S&P, mas nos anos ‘80 o maior mercado era o Japonês. Se tivesssemos investido no mercado accionista Japonês no fim dos anos ‘80 só agora estariamos a recuperar o nosso capital.

Nota sobre o mercado Japonês:

Os mais atentos poderão saber que o máximo do Nikkei 225 (indíce Japonês) em ‘89 foi nos 39 mil pontos e actualmente só se encontra nos 27 mil pontos. Contudo o nikkei é um indíce de preço (como S&P 500), isto é não toma em consideração os dividendos e não representa o retorno total.

6.3 - Look Ahead Bias#

Análise que inclui dados que não estavam disponíveis na altura. Por exemplo fazer uma análise qualitativa de empresas com base nos resultados/balanço de determinado ano e comprar ou vender com base nisso. Na realidade os balanços das empresas só estão disponíveis muitas vezes meses depois do fecho do seu ano fiscal. Resumindo, estariamos a usar dados que na altura que teriamos de tomar a decisão ainda não estavam disponíveis.

6.4 - Time Period Bias#

Quando fazemos uma análise o período de tempo da mesma é extremamente relevante. Por exemplo o famoso ETF IWDA (tracker do MSCI World) começou no final de 2009, que coincidiu com o início de um bull market. O performance no período em análise estará, naturalmente, sobrevalorizada. A performance do IWDA desde essa altura é cerca de 12%/ano, acima da performance de longo prazo do MSCI World.

Se por outro lado escolhermos a data de início do MSCI World em EUR (1999), vai cinincidir com o fim de um Bull Market e início de uma das piores décadas de sempre para o mercados accionista, a primeira década de 2000. O retorno foi de “apenas” 6%, por sua vez abaixo do retorno de longo prazo do MSCI World.

Devemos contudo ter em atenção que muitas vezes o uso de todos os dados possíveis poderá não ser a melhor decisão ou trazer nada de novo excepto complexidade. Considera-se que muitos mercados accionista sofreram um alteração estrutural na segunda guerra mundial, sendo que muitas vezes as análises só começam em 1950 (o que por sua vez não invalida o estudo do passado). Um bom conhecimento empírico do que estamos a analisar é importante para percebermos as nuances dos dados e os erros em que poderemos incorrer.