Capítulo 4 -Distribuições de probabilidades

Capítulo 4 -Distribuições de probabilidades#

As probabilidades desempenham um papel crítico nas decisões de investimento. Embora não possamos prever o futuro, as decisões de investimento informadas são baseadas em algum tipo de probabilidade, trabalhando com variáveis aleatórias. Uma distribuição de probabilidade especifica as probabilidades associadas com os resultados possíveis de uma variável aleatória.

Variáveis aleatórias#

Uma variável aleatória é uma quantidade cujos resultados futuros são incertos (ex: os retornos de uma acção). Os dois mais básicos tipos de variáveis aleatórias são variáveis aleatórias discretas e variáveis aleatórias contínuas.

Variáveis aleatórias discretas#

Uma variável aleatória discreta pode assumir no máximo um número contável (possivelmente infinito) número de valores possíveis. O volume de uma acção é um exemplo de uma variável aleatória discreta. É um número “contável”.

Variáveis aleatórias contínuas#

Por outro lado, não podemos contar os resultados de uma variável aleatória contínua. A taxa de retorno de um investimento é um exemplo de uma variável aleatória contínua. Pode assumir qualquer valor numa sequência. Tanto pode ser 1.0% como 1.0001% e qualquer número entre eles (infinitos).

Distribuições de probabilidade#

Cada variável aleatória está associada a uma distribuição de probabilidade que descreve completamente a variável. Podemos visualizar uma distribuição de probabilidade de duas maneiras. O básico é a função de probabilidade, que especifica a probabilidade de que o variável assume um valor específico (em inglês Probability density function ou pdf). Podemos, também, usar a função de distribuição acumulativa, que nos dá a probabilidade de que uma variável aleatória X seja menor ou igual a um determinado valor x, P(X ≤ x) (em inglês cumulative density function ou cdf).

Distribuição Uniforme Discreta#

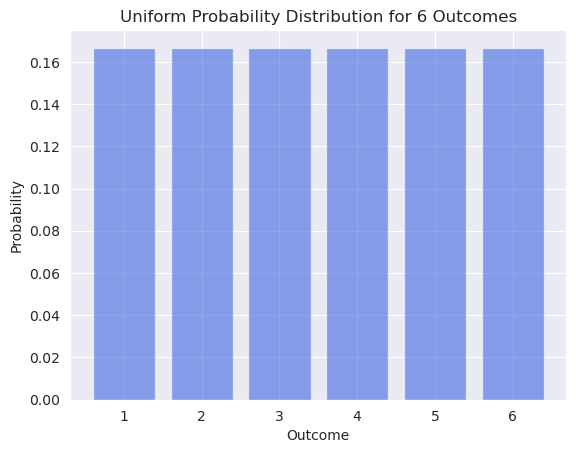
A mais simples de todas as distribuições é a distribuição uniforme discreta. A distribuição tem um número finito de possibilidades e todas as possibilidades têm a mesma probabilidade.

Tabela de Probabilidade para um dado. 6 possibilidades, cada uma delas com a mesma probabilidade:

Características do pdf#

$ 0 \le p(x) \le 1 $

Soma das probabilidades é 1

_images/549116d1b7e72e3d8922f60a8e2f268c40cdf88158c8a00afc91651dbfc14cfc.png

Características do cdf#

$0\le F(x) \le 1$
À medida que aumentamos $x$ o cdf aumenta ou mantém-se constante (por ser acumulativa nunca pode descer)

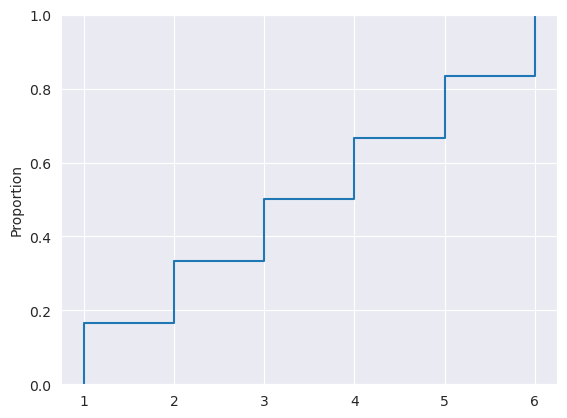
_images/488bc4f41eaf6191e0f8b0dabec0303a6031b099a913020d0d07c119116c09d4.png

Usando as funções para calcular os valores do quadro:

Função Probabilidade

Como numa distribuição uniforme todos os eventos têm a mesma probabilidade podemos calcular $P(E) = \frac{1}{N}$, onde E é o evento e N o número de possibilidades. Neste caso $P(QualquerNúmeroDoDado) = \frac{1}{6}$

Função de distribuição acumulativa

Questão:

Para um distribuição normal de 20 possibilidades (números inteiros de 1 a 20) qual é a probabilidade de X ser maior ou igual a 3 mas menor ou igual a 5 ($P(3\geq X \le 5)$)?

Para calcularmos a probabilidade entre valores podemos calcular a soma das probabilidades entre esses valores:

Criando as funções python para a distribuição uniforme discreta:

import scipy
from scipy import stats
import numpy as np

def compute_uniform_pdf(min_value, max_value, step=1):
    return scipy.stats.uniform.pdf(np.arange(min_value, max_value+1, step), min_value, max_value)[0]

def compute_uniform_cdf(min_value, max_value, step=1):
    return scipy.stats.uniform.cdf(np.arange(min_value+1, max_value+2, step), min_value, max_value)

np.round(compute_uniform_pdf(min_value=1, max_value=6, step=1), 4)

0.1667

np.round(compute_uniform_cdf(min_value=1, max_value=6, step=1), 4)

array([0.1667, 0.3333, 0.5   , 0.6667, 0.8333, 1.    ])

Podemos fazer a soma das 3 probabilidades individuais:

compute_uniform_pdf(min_value=1, max_value=20, step=1) * 3

0.15000000000000002

ou $P(X \le 5) - P(X \le 2)$

compute_uniform_cdf(min_value=1, max_value=20, step=1)

array([0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 , 0.55,
       0.6 , 0.65, 0.7 , 0.75, 0.8 , 0.85, 0.9 , 0.95, 1.  ])

# Lembrem-se que python começa a contar desde o zero
compute_uniform_cdf(min_value=1, max_value=20, step=1)[4] - compute_uniform_cdf(min_value=1, max_value=20, step=1)[1]

0.15

Distribuição Binomial#

Em muitos contextos de investimento podemos ver os resultados de forma binária, sucesso ou perda, subida ou queda. Esta forma de vermos as coisas vai-nos ajudar nos cálculos e é a base de preço de opções (e da origem à árvore de probabilidades que calculamos no capítulo 3).

A base da distribuição binomial é aquilo a que chamamos tentativa de bernoulli. Uma tentativa de bernoulli é um binomial, os resultados são exclusivamente sucesso ou fracasso, cara ou coroa, 1 ou 0.

Assim sendo a função probabilidade de uma tentativa de Bernoulli é:

P(1) = p
P(0) = 1-p (o inverso)

onde p é a probabilidade de sucesso

Características#

A probabilidade p, se sucesso, é constante para todas as tentativas;
As tentativas são independentes;
No caso de p ser 0.5 a distribuição binomial vai ser simétrica (como a distribuição normal).

Para definirmos uma distribuição binomial precisamos por isso de duas variáveis, p, a probabilidade de sucesso e n, o números de tentativas.

Distribuições em python usando o numpy random: https://deepnote.com/@luisilva/Distribuicoes-c1aa98e2-11b8-4472-ac99-5f4f80f0f7c7

Exemplo#

Um tipo de distribuição binomial muito usada é sucesso caso a acção suba e fracasso caso a acção desça. Sabendo p e n podemos calcular as probabilidades dos movimentos e caminhos que o preço da acção pode tomar. Exemplo coo 4 passos/eventos.

Como calcular o número de caminhos possíveis?

Não é mais do que calcular pares ordenados usando Combinações.

from sympy.functions.combinatorial.numbers import nC, nP

tentativas = 4
movimentosDeSubida = 0

nC(tentativas,movimentosDeSubida)

\[\displaystyle 1\]

tentativas = 4
movimentosDeSubida = 3

nC(tentativas,movimentosDeSubida)

\[\displaystyle 4\]

Como calcular a probabilidade individual de cada caminho?

Não é mais do que P(E) = 1/N, sendo N a quantidade de caminhos possíveis.

float(1/(nC(5,0) + nC(4,1) + nC(4,2) + nC(4,3) + nC(4,4) + nC(4,5)))

0.0625

Como calcular as probabilidades

Criando as fórmulas em python:

# Referência: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.binom.html

def compute_binomial_pmf(p, n, k):
    '''
    p = probabilidade de sucesso
    n = número de tentativas
    k = número de sucessos
    '''
    return scipy.stats.binom.pmf(p=p, n=n, k=k)

def compute_binomial_cdf(p, n, k):
    '''
    p = probabilidade de sucesso
    n = número de tentativas
    k = número de sucessos
    '''
    return scipy.stats.binom.cdf(p=p, n=n, k=k)

Probabilidade de cada evento

compute_binomial_pmf(p=0.5, n=4, k=2)

0.375

Probabilidades cumulativas

compute_binomial_cdf(p=0.5, n=4, k=2)

0.6875

Como calcular a variância e desvio padrão??

Criando as fórmulas em python:

def compute_binomial_var(p, n):
    '''
    p = probabilidade de sucesso
    n = número de tentativas
    '''
    return scipy.stats.binom.var(p=p, n=n)

def compute_binomial_std(p, n):
    '''
    p = probabilidade de sucesso
    n = número de tentativas
    '''
    return scipy.stats.binom.std(p=p, n=n)

Nos últimos 10 anos a empresa Y aumentou a facturação anual 7 vezes. Se decidirmos modelar os aumentos de facturação da próxima década usando uma distribuição binomial:

A) Qual a probabilidade de aumentar a facturação em cada ano?

$ P(af) = 7/10 $

B) Qual a probabilidade de a facturação aumentar exactamente 5 dos 10 anos

compute_binomial_pmf(p=0.7, n=10, k=5)

0.10291934519999998

C) Calcule a variância e o desvio padrão da distribuição

Variância:

compute_binomial_var(0.7, 10)

2.1000000000000005

Desvio padrão:

compute_binomial_std(0.7, 10)

1.449137674618944

Distribuição Uniforme Contínua#

Se na secção anterior consideramos variáveis aleatórias discretas, que por definição são “contáveis”, vamos agora considerar variáveis aleatórias contínuas, que não são “contáveis”.

Tal como na distribuições de variáveis discretas a a distribuição uniforme é a mais simples de entender e prova ser um bom ponto de início.

Quando estávamos a trabalhar com variáveis aleatórias discretas conseguíamos atribuir uma determinada probabilidade a cada evento. Com variáveis aleatórias contínuas tal não vai ser possível, pois há uma infinidade de eventos. Por isso a probabilidade de cada valor específico é de 0.

Iremos por isso apenas trabalhar com o CDF, a função de distribuição acumulativa.

import matplotlib.pyplot as plt
import seaborn as sns

plt.style.use('seaborn-v0_8')

sns.lineplot(x=[1, 10], y=[0, 1]);

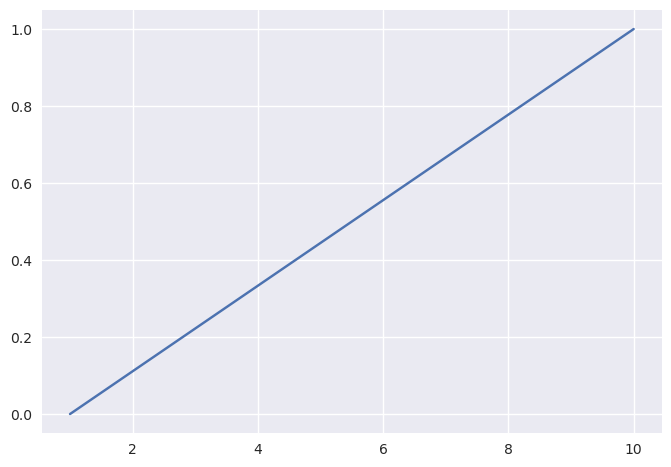
_images/a518b77fa87b52efbab7b219745a16e3f7373c06a0568d5ff98c1986dc92fbfb.png

O vamos precisar de saber:

O CDF da distribuição uniforme contínua (tal como na versão discreta) sobe linearmente;
A probabilidade de cada ponto discreto é 0;
A probabilidade acumulativa continua a ser entre 0 e 1;
A probabilidade acumulativa entre dois pontos é a probabilidade acumulativa do ponto à mais à direita menos a probabilidade acumulativado ponto mais à esquerda: $4 \le X \le 6 = F(6) - F(4)$

Questão

Estamos a tentar prever as vendas de uma companhia no quarto trimestre do ano fiscal. As nossas estimativas estão entre 14 mil e 15 mil euros de vendas. Decidimos tratar todas as possibilidades como tendo a mesma probabilidade e por isso usamos a distribuição uniforme contínua.

Qual é o retorno médio esperado?
Qual é a probabilidade de a empresa ter 14.125 euros ou menos em vendas no quarto trimestre?
Qual a probabilidade de as vendas serem entre 14250 e 14625 euros?

Resolução

CDF

sns.lineplot(x=[14000, 15000], y=[0, 1]);

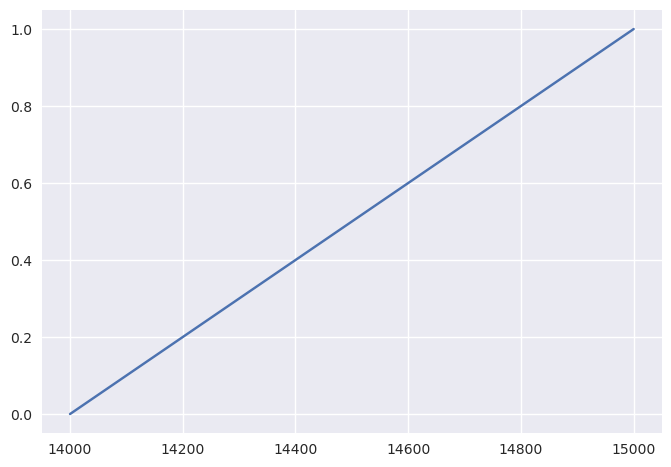
_images/cd164f3ed28dddc5fc9bc7a9cfe96de51a06466d5ee602bab934465b22a12593.png

A. Qual é o retorno médio esperado?

O retorno médio esperado numa distribuição uniforme contínua é a média aritmética entre o valor mínimo e máximo. $\frac {15000+14000} {2} = 14500$

B. Qual é a probabilidade de a empresa ter 14.125 euros ou menos em vendas no quarto trimestre?

A probabilidade da empresa ter 14.125 pode ser calculado com recurso à nossa fórmula compute_uniform_cdf_continuous() que calcula a probabilidade acumulada da distribuição até ao ponto desejado

def compute_uniform_cdf_continuous(min_value, max_value, value):
    if value < max_value and value > min_value:
        return (value - min_value)  / (max_value - min_value)
    else:
        return ("Error: value is probably not betwwen the min and max values")

compute_uniform_cdf_continuous(14000, 15000, 14125)

0.125

C. Qual a probabilidade de as vendas serem entre 14250 e 14625 euros?

F_14750 = compute_uniform_cdf_continuous(14000, 15000, 14625)
F_14250 = compute_uniform_cdf_continuous(14000, 15000, 14250)

F_14750 - F_14250

0.375

Distribuição Normal#

A distribuição normal é possivelmente a distribuição de probabilidade mais usada em trabalho quantitativo. Desempenha um papel importante em Modern Portfolio Theory e em gestão de risco. Por ter tantos usos, a distribuição normal deve ser completamente compreendido pelos profissionais de investimento.

O papel da distribuição normal na inferência estatística e na análise de regressão é amplamente estendido por um resultado crucial conhecido como o teorema do limite central. A Central O teorema do limite afirma que a soma (e a média) de um grande número de variáveis (com variância finita) é aproximadamente normalmente distribuída.

Características#

A distribuição normal:

é completamente descrita por dois parâmetros - a sua média ($\mu$) e a sua variância ($\sigma$);
é simétrica e em formato de sino;
tem uma assimetria (Skewness) de 0;
tem uma curtose (Kurtosis ) de 3, e/ou uma curtose em excesso de 0;
tem média, mediana e moda iguais;

Distribuição univariada e multivariada#

Uma distribuição univariada descreve apenas uma variável aleatória (os retornos de uma acção). Por outro lado uma distribuição multivariada especifica a probabilidade de um grupo de de variáveis aleatórias relacionadas (o retorno de um portefólio de 20 acções).

Neste último caso temos não só de tomar em consideração cada variável aleatória individual mas também toda as relações estatística entre elas (no caso de um portefólio de acções teremos de ter em consideração as covariâncias entre as acções).

Uma distribuição normal multivariada é assim definida por 3 listas de parâmetros:

Uma lista dos retornos médios de cada variável aleatória;
Uma lista das variâncias;
Uma lista de todas as covariâncias entre as variáveis aleatórias.

Distribuição normal standard#

Há tantas distribuições normais quantas combinações de diferentes médias ($\mu$) e variâncias ($\sigma$). Mas devido às características da distribuição normal é comum trabalharmos só com a distribução normal standard. A distribuição normal standard é uma distribuição normal com um desvio padrão de 1 e uma média de 0.

Quando temos que trabalhar com outras distribuições normais o procedimento que tomamos é standartizar essa distribuição, de forma a trabalhar com ela como se tivesse sido um standard desde o início.

Embora não podendo levar de uma forma literal e sendo apenas uma forma aproximada a distribuição normal é comummente usada como a distribuição para os retornos de um activo ou portefólio. Um desvio da normalidade na maioria dos retornos de acções é que na realidade a distribuição dos retornos tem um curtose superior a 3, como vimos no capítulo 2. Há, assim, um problema desta distribuição ter caudas mais gordas do que a distribuição normal.

Como consequência o uso da distribuição normal para modelarmos retornos tenderá a subestimar a probabilidade de retornos extremos.

É importante dar enfase que o uso da distribuição normal se deve focar nos retornos, pois não é o modelo indicado para modelar preços. Uma variável aleatória normal não tem um limite mínimo o que entra logo em conflito com o facto de um activo só poder descer até 0, preço onde perde todo o seu valor.

Uma grande vantagem de uma distribuição normal advém do facto de ser simétrica e podermos calcular com facilidade as probabilidades:

Aproximadamente 50% das observações caem no intervalo [$\mu +/- \frac{2}{3} \sigma$]
Aproximadamente 68% das observações caem no intervalo [$\mu +/-\sigma$]
Aproximadamente 95% das observações caem no intervalo [$\mu +/- 2\sigma$]
Aproximadamente 99% das observações caem no intervalo [$\mu +/- 3\sigma$]

Standartizar uma distribuição normal#

Devido a haver muitas distribuições normais mas todas terem características semelhantes é normal trabalharmos com a distribuição normal standard, isto é, uma distribuição normal com médio 0 e desvio padrão 1.

O que fazer então quando a variável aleatória não segue uma distribuição normal standard?

Nesse caso passará por um processo de standartização.

Para standardizar X vamos subtrair a média de X a X e dividir o resultado pelo seu desvio padrão. Assim desta forma [$Z = \frac{X - \mu} {\sigma}$]

Exemplo:

Vamos supôr que temos uma variável aleatória X, com $\mu$ = 5 e $\sigma$ = 0. Vamos standartizar $X$ com $Z = \frac{X - 5}{1.5}$. Desta forma a um valor de $X = 9.5$ corresponde um valor standardizado de 3 ($Z = \frac{9.5 - 5}{1.5} = 3$).

Podemos assim responder a todas as questões probabilísticas sobre $X$ usando valores standartizados e as tabelas de probabilidade de $Z$.

Muitas vezes não sabemos $\mu$ e $\sigma$, pois são valores que dizem respeito à população. Usamos então $\tilde{x}$ e $s$ respectivamente, que são os valores equivalentes na amostra.

Para uso da distribuição normal é comum usar uma tabela que nos dá a probabilidade de $Z \le x$

Para descobrir a probabilidade que uma variável normal standard seja igual ou inferior a 0.24, por exemplo, pesquisamos a linha com 0.20 e a coluna 0.04, para descobrirmos a entrada 0.5948. Assim, $Z \le 0.24 = 0.5948$ ou 59.48%

Usando python

Para descobrirmos as probabilidades de $Z \le x$ usado python introduzimos directamente os valores, nem precisando de normalizar se estivermos a tabalhar com uma variável normal não standard.

Podemos já repetir o exercício em cima e introduzir os dados para $Z \le 0.24$

scipy.stats.norm(0, 1).cdf(0.24)

0.5948348716977958

vamos também confirmar que, como calculado em cima, $X \sim {\sf N}(5, 1.5)$ é equivalente a $Z \sim {\sf N}(0, 1)$ quando $N$ = 9.5 e $Z=3$

scipy.stats.norm(0, 1).cdf(3)

0.9986501019683699

# Transformando em função
def compute_normal_cdf(mu, std, value):
    return scipy.stats.norm(mu, std).cdf(value)

compute_normal_cdf(5, 1.5, 9.5)

0.9986501019683699

Exercício 4.1

Se um portefólio tiver uma rentabilidade média de 10% e um desvio padrão de 18% ao ano e assumindo que os retornos seguem uma distribuição normal:

Qual a probabilidade do retorno exceder 20%?
Qual a probabilidade do retorno estar entre 12 e 20%?
Qual a probabilidade de retorno do portfolio ser igual ou inferior a 5.5%?

# 1
# Lembrem-se que o cdf é a probablidade de 0 até ao valor alvo.
# Se queremos a percentagem acima do valor alvo é:
# 1 (probabilidade total) - probabilidade até ao valor alvo

1 - compute_normal_cdf(10, 18, 20)

0.2892573607539719

# 2
# Probabilidade entre dois pontos

compute_normal_cdf(10, 18, 20) - compute_normal_cdf(10, 18, 12)

0.1665067582007167

# 3
# Aqui sim, probabilidade até ao valor alvo

compute_normal_cdf(10, 22, 5.5)

0.41896363758133803

Aplicações da distribuição normal#

Modern Portfolio Theory#

Modern portfolio theory é uma das teorias que faz amplo uso da distribuição normal e baseia-se numa análise média-variancia, como medidas importantes para calcularmos o valor de um investimento.

MPT assume que as rentabilidades são normalmente distribuídas. Embora tal não seja literalmente a realidade é suficientemente aproximada para não invalidar a análise.

Retorno mínimo aceitável#

Podemos utilizar a distribuição normal para calcularmos a probabilidade de determinado porfolio ter um retorno inferior (ou superior) a determinado retorno que achemos que é o objectivo mínimo.

Exemplo

Um investidor tem como objectivo a manutenção do poder de compra do seu portefólio e por isso o objectivo mínimo de retorno é a inflação esperada, que é de 2%.

O investidor tem como opções dois portefólios:

Portefólio 1, com média de 6% e desvio padrão de 8%;
Portefólio 2, com média de 8% e um desvio padrão de 14%.

Qual o portefólio com maior probabilidade de ter um retorno mínimo de 2%?

Portefólio 1:

1 - compute_normal_cdf(6, 8, 2)

0.6914624612740131

Portfólio 2:

1 - compute_normal_cdf(8, 14, 2)

0.6658824291023754

Como podemos ver o portefólio com maior probabilidade de não atingir o objectivo mínimo de retorno de 2% é o portefólio 2. Devemos por isso escolher o portfolio 1, pois tem maior probabilidade de ter um retorno igual ao superior a 2%. O Exemplo é para mostrar que mesmo que um portfolio tenha maio retorno esperado SE a volatilidade aumentar muito pode não compensar irmos para esse portfolio porque há maior probabilidade de atingirmos o nosso objectivo com um portfolio com menor retorno esperado.

P.S. Uma vez que o compute_normal_cdf(6, 8, 2) calcula a probabilidade à esquerda, ou seja, até ao objectivo de 2%, se quisermos saber a probabilidade de ter um retorno igual ou maior que o objectivo (à direita) temos de fazer 1 - compute_normal_cdf(8, 14, 2)

Rácio Safety-First#

O rácio de Safety-First tem uma ideia muito semelhante à do retorno mínimo aceitável. Ou seja, tendo em consideração a média, desvio padrão e retorno desejado a carteira com menor probabilidade de falhar esse objectivo mínimo vai ter um rácio Safety-First superior.

$SFR = \frac{E(R_P-R_L)}{\sigma_p}$

onde $R_p$ é o retorno médio do portefólio, $R_L$ é o valor mínimo desejado e $\sigma_p$ é o desvio padrão do portefólio.

Transformando em fórmula python:

def compute_srf(mean, std, minimum_value):
    return (mean - minimum_value) / (std)

Pegando nas carteiras 1 e 2 do exemplo anterior.

Portefólio 1:

srf_portfolio_1 = compute_srf(6, 8, 2)
srf_portfolio_1

0.5

Portefólio 2:

srf_portfolio_2 = compute_srf(8, 14, 2)
srf_portfolio_2

0.42857142857142855

Como esperado chegamos à mesma conclusão que no exemplo anterior, pois o portefólio 1 apresenta um rácio de Safety First superior. O investidor deve assim escolher o portefólio 1. Em linha com a conclusão da análise com as probabilidades.

VaR e Testes de stress#

Outras situações em que usamos a distribuição normal é em análise de risco.

VaR: É uma medida de perda em investimentos. O VaR calcula o valor mínimo de perda esperada num determinado período (dia, mês, ano etc), dada uma determinada probabilidade.

Testes de stress: É uma medida que complementa o VaR e tenta media a perdas estimadas em períodos extremamente desfavoráveis.

Distribuição log-normal#

A distribuição log-normal é uma distribuição bastante relacionadas com a distribuição normal é é bastante usada para modelar a distribuição de probabilidade de acções e outros activos (opções por exemplo, sendo que é usada no modelo Black-Scholes de avaliação de opções).

Uma variável aleatória segue uma distribuição log-normal se o logaritmo dessa variável aleatória segue uma distribuição normal.

Duas distribuições log-normais (diferentes médias e desvios padrões da distribuição associada)

Características:

Sempre positiva, tem 0 como valor mínimo;
Positivamente enviesada, com ma longa cauda à direita.

Estas características tornam-na ideal para modelar o preço de activos. Ao contrário das outras distribuições que estudamos uma distribuição normal é definida pela média e desvio padrão da distribuição normal associada.

Média e variância de uma distribuição log-normal

Supondo que uma variável aleatória normal $X$ tem uma média $\mu$ e uma variância $\sigma^2$ a média e variância da log-normal associada são:

$\mu_L = exp(\mu+0.5\sigma^2)$

$\sigma^2_L = exp(2\mu+sigma^2) \times exp(\sigma^2 - 1)$

Conceitos importantes a saber#

Retorno com capitalização contínua

A capitalização contínua trata o tempo como algo contínuo e ininterrupto, em oposição ao retorno discreto, que trata o tempo como avançando em intervalos finitos (dia, mês, trimestre, ano). O conceito de retorno com capitalização contínua é usado em vários modelos financeiros como o Black-Sholes.

O retorno com capitalização contínua de um activo é o logarítmo de 1 mais o retorno desse período. Por exemplo se observarmos um retorno no período de 4% o retorno contínuo equivalente é ln(1.04) = 0.039221

Questão: O preço de fecho semanal da acções da Apple foram:

Quanto foi o retorno de capitalização contínua do SPY no período?

Valores da yahoo finance ajustados a dividendos

from numpy import log as ln

# Atenção porque o numpy trata o logarítmo natural como log, embora o encontremos muitas vezes escrito na literatura como ln. Ou seja o ln que vemos em livros é tratado como np.log. Podemos fazer "batota" e importar o log do numpy como ln, o que faz com que a função ln seja igual a np.log. Foi o que fiz, para manter o mesmo estilo que o livro do curso

ln(474.96/311.8)

0.4208686333387438

O retorno de capitalização contínua do SPY foi 42.087%.

Diferenças entre capitalização contínua e capitalização discreta

A utilização de capitalização discreta (holding period return) para descobrirmos o valor final de um investimento de $1 envolve multiplicação (1 + taxa de capitalização discreta) enquanto o uso de rentabilidades de capitalização contínua envolve adição.

O que quer isso dizer?

Pegando no exemplo acima

Rentabilidade capitalização contínua = Rentabilidade contínua 2020 + Rentabilidade contínua 2021

r_continua_2021 = ln(474.96 / 368.96)
r_continua_2022 = ln(368.96 / 311.8)

r_continua_2021 + r_continua_2022

0.4208686333387438

hpr_mais_um_2021 = 474.96 / 368.96
hpr_mais_um_2020 = 368.96 / 311.8

hpr_mais_um_2021 * hpr_mais_um_2020

1.5232841565105837

Das rentabilidades para os valores

No caso da HPR

311.8 * 1.5232841565105837

474.96000000000004

No caso da rentabilidade de capitalização contínua aplicamos a fórmula:

$ValorFinal = ValorInicial \times e^r$

import math

311.8 * math.e**(0.4208686333387438)

474.96000000000004

Retornos são independentes e identicamente distribuídos

Este é outra dos pressupostos importantes e necessários para a validade da matemática financeira.

Exemplo da aula

Introdução a simulações de monte-carlo#

Depois de obter uma compreensão das distribuições de probabilidade, podemos melhor perceber uma técnica em que as distribuições de probabilidade desempenham um papel integral. A técnica é chamada simulação de Monte Carlo, e em finanças envolve o uso de software de computador para representar a operação de um sistema financeiro complexo. Uma característica da simulação de Monte Carlo é a geração de um grande número de amostras aleatórias de uma distribuição ou distribuições de probabilidade especificas para representar o papel do risco no sistema. A simulação de Monte Carlo é amplamente utilizada para estimar o risco e o retorno do investimento formulários. Nesta configuração, simulamos o desempenho de ganhos e perdas do portefólio para um horizonte de tempo especificado. Tentativas repetidas dentro da simulação (cada tentativa envolvendo um sorteio de observações aleatórias de uma distribuição de probabilidade) produzem um distribuição de frequência dos retornos da carteira da qual derivam as medidas de desempenho e risco.

Simulação de monte carlo é usada para:

Planeamento;
Desenvolver estimativas de VaR;
Avaliação de activos complexos, nomeadamente algumas opções exóticas
etc

A simulação de monte-carlo é um complemento a métodos analíticos (onde podemos aplicar uma fórmula). Apenas fornece aproximações estatísticas, não resultados certos. Métodos analíticos deverão ser usados quando disponíveis pois não só apresentam valores exactos como nos proporciona um melhor conhecimento de relações causa-efeito.

Simulação de monte-carlo em python

# Set seed faz com que um estado aleatório seja reproduzível
np.random.seed(0)

# Criar 10 valores aleatórios de uma distribuição normal standard
# Referência: https://numpy.org/doc/stable/reference/random/generated/numpy.random.standard_normal.html
np.random.standard_normal(size=10)

array([ 1.76405235,  0.40015721,  0.97873798,  2.2408932 ,  1.86755799,
       -0.97727788,  0.95008842, -0.15135721, -0.10321885,  0.4105985 ])

# Criar 10 valores aleatórios de uma distribuição normal com médio e desvio padrão escolhido por nós
# Referência: https://numpy.org/doc/stable/reference/random/generated/numpy.random.normal.html
portfolio_dp_10 = np.random.normal(loc=0.06, scale=0.10, size=10)
portfolio_dp_10

array([ 0.07440436,  0.20542735,  0.13610377,  0.0721675 ,  0.10438632,
        0.09336743,  0.20940791,  0.03948417,  0.09130677, -0.02540957])

A média de 6% e o desvio padrão de 10% não foi inocente, são valores em linha com uma carteira moderada. Acabamos assim por calcular possíveis retornos aleatórios dessa carteira. Podemos experimentar aumentar o desvio padrão para 25 e ver o resultado.$$

# Criar 10 valores aleatórios de uma distribuição normal com médio e desvio padrão escolhido por nós
# Referência: https://numpy.org/doc/stable/reference/random/generated/numpy.random.normal.html
portfolio_dp_15 = np.random.normal(loc=0.06, scale=0.15, size=10)
portfolio_dp_15

array([-0.32294847,  0.15804279,  0.18966543, -0.05132475,  0.40046319,
       -0.15815485,  0.06686378,  0.03192242,  0.28991688,  0.28040382])

A “carteira” com maior desvio padrão teria um retorno de 62.74% no quinto período. O triplo do melhor “retorno” da carteira com desvio padrão mais baixo

Com um array de retornos podemos construir as séries temporais de uma carteira aleatória onde investimos 100 euros:

# Não chateando com a parte matemática são estas as funções que vamos usar
def compute_time_series(dataframe):

    #    INPUT: Dataframe of returns
    #    OUTPUT: Growth time= series starting in 100

    return ((np.exp(np.log1p(dataframe).cumsum()))) * 100

def merge_time_series(df_1, df_2, how='outer'):
    df = df_1.merge(df_2, how=how, left_index=True, right_index=True)
    return df

def add_row_on_top(df, new_row):
    df.loc[-1] = new_row  # adding a row
    df.index = df.index + 1  # shifting index
    df = df.sort_index()  # sorting by index
    return df
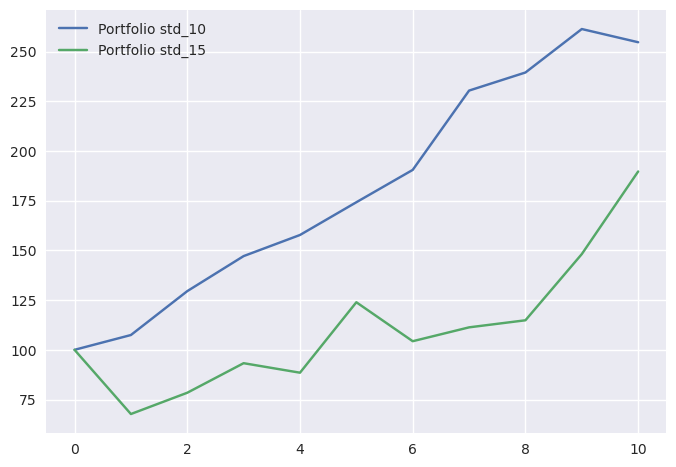
portfolio_dp_10_df = compute_time_series(pd.DataFrame(portfolio_dp_10))

portfolio_dp_15_df = compute_time_series(pd.DataFrame(portfolio_dp_15))

time_series = merge_time_series(portfolio_dp_10_df, portfolio_dp_15_df)

time_series = add_row_on_top(time_series, [100, 100])

time_series.columns = ['Portfolio std_10', 'Portfolio std_15']

time_series.plot();

_images/e867a130735d637fceb7ce772e6c0b0bcc085c36a7d6717ce21ea3cc86f05c4d.png

Exemplos: https://tinyurl.com/hkv7vkv2

Capítulo 4 -Distribuições de probabilidades

Contents

Capítulo 4 -Distribuições de probabilidades#

Variáveis aleatórias#

Variáveis aleatórias discretas#

Variáveis aleatórias contínuas#

Distribuições de probabilidade#

Distribuição Uniforme Discreta#

Características do pdf#

Características do cdf#

Distribuição Binomial#

Características#

Exemplo#

Distribuição Uniforme Contínua#

Distribuição Normal#

Características#

Distribuição univariada e multivariada#

Distribuição normal standard#

Standartizar uma distribuição normal#

Aplicações da distribuição normal#

Modern Portfolio Theory#

Retorno mínimo aceitável#

Rácio Safety-First#

VaR e Testes de stress#

Distribuição log-normal#

Conceitos importantes a saber#

Introdução a simulações de monte-carlo#