Capítulo 7 - Regressão Linear Simples#
A saber:
O que é uma regressão linear simples e para o que serve;
Distinguir a variável dependente da independente;
Como calcular uma regressão linear simples;
Importância e cálculo da inclinação, intercept, \(r^2\);
Teste de hipótese de inclinação ser diferente de 0
Há funções novas
Show code cell source
import plotly.express as px
import yfinance as yf
import pandas as pd
from scipy import stats
import numpy as np
def merge_time_series(df_1, df_2, how='outer'):
df = df_1.merge(df_2, how=how, left_index=True, right_index=True)
return df
def normalize(df):
df = df.dropna()
return (df / df.iloc[0]) * 100
def download_yahoo_data(tickers, normalize_quotes=True,
start='1970-01-01', end='2030-12-31'):
quotes=pd.DataFrame()
for ticker in tickers:
df = yf.download(ticker, start=start, end=end, progress=False)
df = df[['Adj Close']]
df.columns=[ticker]
quotes = merge_time_series(quotes, df)
quotes = quotes.ffill()
if normalize_quotes:
quotes = normalize(quotes)
return quotes
def compute_g(FV, PV, N):
g = ((FV/PV)**(1/N))-1
return g
def compute_diference_in_years(start, end):
start_date = pd.to_datetime(start)
end_date = pd.to_datetime(end)
difference = end_date - start_date
difference_in_years = (difference.days)/365.2421
return difference_in_years
def compute_FV_lump_sum(PV, r, N):
'''
FV = Future value / valor futuro
PV = Present value / Valor presente
r = Interest rate rate / Taxa de juro
N = Número de períodos de capitalização
'''
FV = PV * (1+r)**N
return FV
def compute_regression_coeficients(x, y):
return stats.linregress(x=x, y=y)
def compute_regression_value(x, y, x_value):
slope, intercept, r, p, std_err = stats.linregress(x, y)
return slope * x_value + intercept
def compute_regression_line(x, y):
slope, intercept, r, p, std_err = stats.linregress(x, y)
def compute_regression_value_helper_function(x):
return slope * x + intercept
return list(map(compute_regression_value_helper_function, x))
def create_regression_dataframe(x, y):
regression_line = compute_regression_line(x, y)
df = pd.DataFrame()
df['Y'] = list(y)
df['X'] = list(x)
df['Regression'] = list(regression_line)
return df
def compute_coefficient_of_determination(squares_reg, sum_squares_total):
'''
squares regression/sum of squares total
'''
return squares_reg/sum_squares_total
def compute_std_error_reg(mean_squared_error):
return np.sqrt(mean_squared_error)
Exemplo de Regressão linear nos mercados a longo prazo#
Fonte: Stocks for the Long Run by Jeremy J. Siegel (Sixth Edition)
Em análise financeira por vezes percisamos de de verificar se uma variável é útil para explicar outra variável. Se, por exemplo, a valorização da cotação do petróleo tem impacto na valorização de da cotação de uma empresa petrolífera, e se sim em média qual é o impacto esperado. Resumindo se o petróleo subir 1% qual o impacto esperado na cotação da empresa.
Mas isso só se pode calcular se houver uma relação entre as variáveis (neste caso a variação da cotação do petróleo e a cotação da empresa petrolífera).
Exemplo do Livro (Exhibit 2 página 529)#
Um analista acredita que o CAPEX do ano anterior têm impacto na variável ROA e decide testar isso. Qual a variável dependente e independente?
Show code cell source
df = pd.DataFrame()
df['Y'] = [6.0, 4.0, 15.0, 20.0, 10.0, 20.0]
df['X'] = [0.7, 0.4, 5.0, 10.0, 8.0, 12.5]
df
| Y | X | |
|---|---|---|
| 0 | 6.0 | 0.7 |
| 1 | 4.0 | 0.4 |
| 2 | 15.0 | 5.0 |
| 3 | 20.0 | 10.0 |
| 4 | 10.0 | 8.0 |
| 5 | 20.0 | 12.5 |
Show code cell source
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('seaborn-v0_8')
# Set the plot size
plt.figure(figsize=(12, 6))
# Create the scatter plot
sns.scatterplot(data=df, x='X', y='Y', s=150) # 's' sets the marker size (adjusted to be larger)
# Set plot titles and labels
plt.title("Scatter plot ROA/CAPEX")
plt.xlabel("CAPEX (%)")
plt.ylabel("ROA (%)")
# Customize the y-axis range and add percentage formatting to both axes
plt.ylim(0, 22)
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda y, _: f'{y:.0f}%'))
plt.gca().xaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'{x:.0f}%'))
# Show the plot
plt.show()
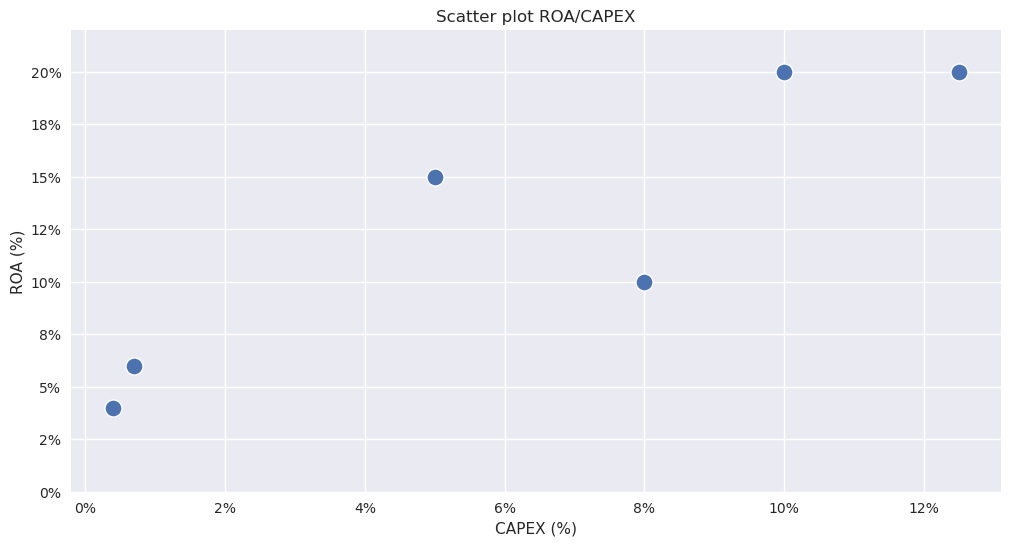
Estimação da regressão linear simples#
Show code cell source
# Set the plot size
plt.figure(figsize=(12, 6))
# Create the scatter plot with a regression line
sns.regplot(
data=df,
x='X',
y='Y',
scatter_kws={'s': 150}, # Increase marker size
line_kws={'color': 'black'}, # Trendline color
ci=None # Removes confidence interval shading, similar to Plotly's OLS trendline
)
# Set plot titles and labels
plt.title("Scatter plot ROA/CAPEX, com regressão linear OLS")
plt.xlabel("CAPEX (%)")
plt.ylabel("ROA (%)")
# Customize the y-axis range and add percentage formatting to both axes
plt.ylim(0, 22)
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda y, _: f'{y:.0f}%'))
plt.gca().xaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'{x:.0f}%'))
# Show the plot
plt.show()
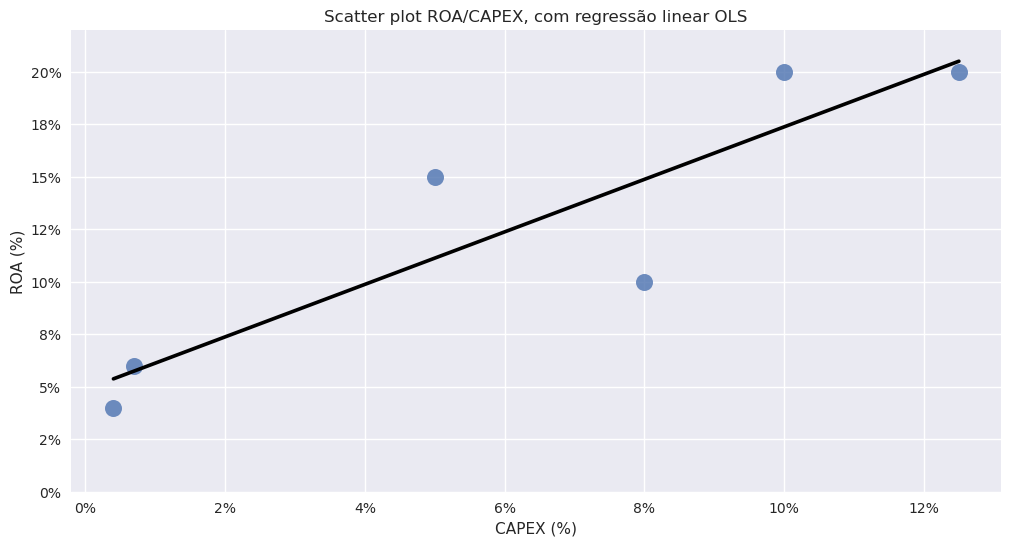
A recta é onde o somatório do quadrado das distâncias para a média é menor. No gráfico podemos ver os resíduos.
## PYTHON QUE TEM DE SE SABER
y = [6.0, 4.0, 15.0, 20.0, 10.0, 20.0]
x = [0.7, 0.4, 5.0, 10.0, 8.0, 12.5]
create_regression_dataframe(y=y, x=x)
| Y | X | Regression | |
|---|---|---|---|
| 0 | 6.0 | 0.7 | 5.750 |
| 1 | 4.0 | 0.4 | 5.375 |
| 2 | 15.0 | 5.0 | 11.125 |
| 3 | 20.0 | 10.0 | 17.375 |
| 4 | 10.0 | 8.0 | 14.875 |
| 5 | 20.0 | 12.5 | 20.500 |
Interpretação dos coeficientes da regressão#
## PYTHON QUE TEM DE SE SABER
compute_regression_coeficients(x=df['X'], y=df['Y'])
LinregressResult(slope=1.25, intercept=4.874999999999999, rvalue=0.894485541601211, pvalue=0.01611258928781205, stderr=0.31239805904148915, intercept_stderr=2.3719633958885398)
Slope - Inclinação da recta#
Positiva, variáveis têm relação positiva
Negativa, variáveis têm relação negativa
Próxima de 0, variáveis não têm relação
Intercept#
Valor de Y quando X=0
Rvalue - Força da relação#
Costuma-se usar o R^2 que é o coeficiente de determinação
*”Expressa a quantidade da variância dos dados que é explicada pelo modelo linear. Assim, quanto maior o R², mais explicativo é o modelo linear, ou seja, melhor o modelo ajusta à amostra. Por exemplo, um R² = 0,8234 significa que o modelo linear explica 82,34% da variância da variável dependente a partir do regressores (variáveis independentes) incluídas naquele modelo linear. “
Previsões#
Sabendo o slope e a interception podemos fazer a recta, usando qualquer valor de x na equação da mesma:
\(y = mx + b\)
Isso faz com que também possamos fazer estimativas ou previsões, onde seja, onde estaria a recta para um determinado valor de \(x\)
1.25 * 5 + 4.875
11.125
## PYTHON QUE TEM DE SE SABER
compute_regression_value(x=x, y=y, x_value=5)
11.125
# Onde estaria a recta para todos os valores de x entre 0 e 20?
for x_value in range(20):
print(compute_regression_value(x=x, y=y, x_value=x_value))
4.874999999999999
6.124999999999999
7.374999999999999
8.625
9.875
11.125
12.375
13.625
14.875
16.125
17.375
18.625
19.875
21.125
22.375
23.625
24.875
26.125
27.375
28.625
Exemplo 3 (página 539)#
Um analista estimou um modelo de regressão entre o retorno sobre o patrimônio líquido de uma empresa (ROE) contra suas oportunidades de crescimento (GO), definidas como a taxa de crescimento anual composto de três anos da empresa em vendas, ao longo de 20 anos e estima a seguinte regressão linear simples:
\(ROEi = 4 + 1.8 GOi + εi\) . Ambas as variáveis são expressas em percentagens, por isso uma observação GO de 5% é 5.
1 - O valor previsto do ROE da empresa se seu GO for 10% é o mais próximo de:
A) 1,8%
B) 15,8%
C) 22,0%
2 A mudança no ROE para uma mudança no GO de 5% para 6% é mais próxima de:
A) 1,8%
B) 4,0%
C) 5,8%
3 O residual no caso de um GO de 8% e um ROE observado de 21% é mais perto de:
A) -1,8%
B) 2,6%
C) 12,0%
Soluções
Show code cell source
# C está correta. O valor previsto do ROE = 4 + (1,8 × 10) = 22.
# A está correta. O coeficiente de inclinação de 1,8 é a mudança esperada na variável dependente (ROE) para uma mudança de uma unidade na variável independente (GO).
# B está correta. O valor previsto é ROE = 4 + (1,8 × 8) = 18,4. O valor observado do ROE é 21, portanto, o residual é 2,6 = 21,0 − 18,4.
Presupostos do modelo de regressão linear simples#
1. Linearidade - A Relação entre a variável dependente, Y, e a variável independente, X, é linear;
2. Homocedasticidade - A vâriancia para os resíduos da regressão é constante;
3. Independência - As observações são independentes
4. Normalidade - Os resíduos da regressão são normalmente distribuidos
Pressuposto 1 - Linearidade#
O modelo de regressão linear simples é um modelo linear por isso estamos a assumir uma relação linear entre as variáveis. Nem todas as variáveis têm uma relação linear. Um exemplo comum disso é uma relação exponencial.
Show code cell source
# Create the DataFrame
df = pd.DataFrame()
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = x + np.random.randint(-3, 3, 10)
df['X'] = x
df['Y'] = y
# Set the plot size
plt.figure(figsize=(12, 6))
# Create the scatter plot
sns.scatterplot(data=df, x='X', y='Y', s=150) # 's' sets the marker size (adjusted to be larger)
# Set plot titles and labels
plt.title("Relação Linear")
plt.xlabel("Variável independente (%)")
plt.ylabel("Variável dependente (%)")
# Customize the axes to show percentage signs
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda y, _: f'{y:.0f}%'))
plt.gca().xaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'{x:.0f}%'))
# Show the plot
plt.show()
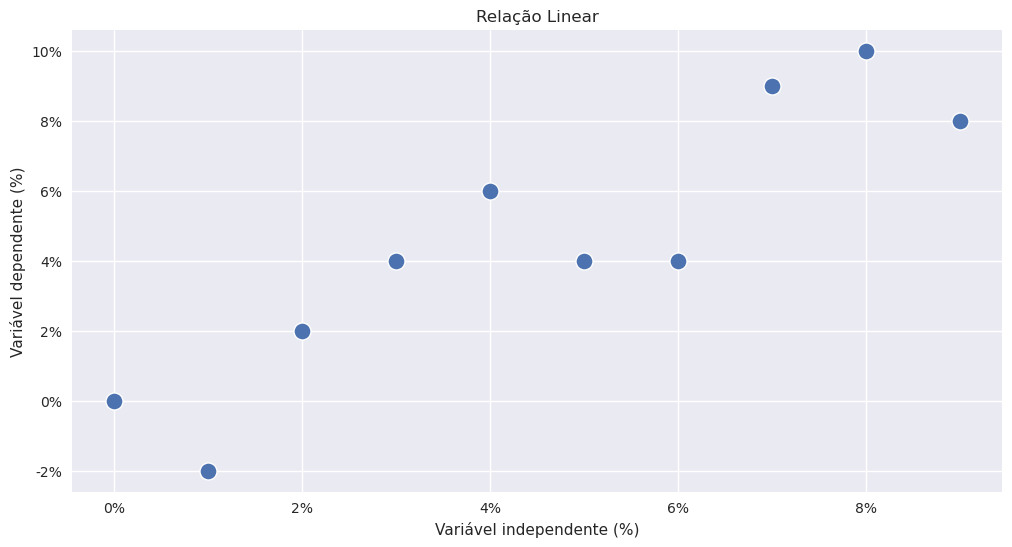
Show code cell source
# Create the DataFrame
df = pd.DataFrame()
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = x ** 3
df['X'] = x
df['Y'] = y
# Set the plot size
plt.figure(figsize=(12, 6))
# Create the scatter plot
sns.scatterplot(data=df, x='X', y='Y', s=150) # 's' sets the marker size (adjusted to be larger)
# Set plot titles and labels
plt.title("Relação Exponencial")
plt.xlabel("Variável independente")
plt.ylabel("Variável dependente")
# Show the plot
plt.show()
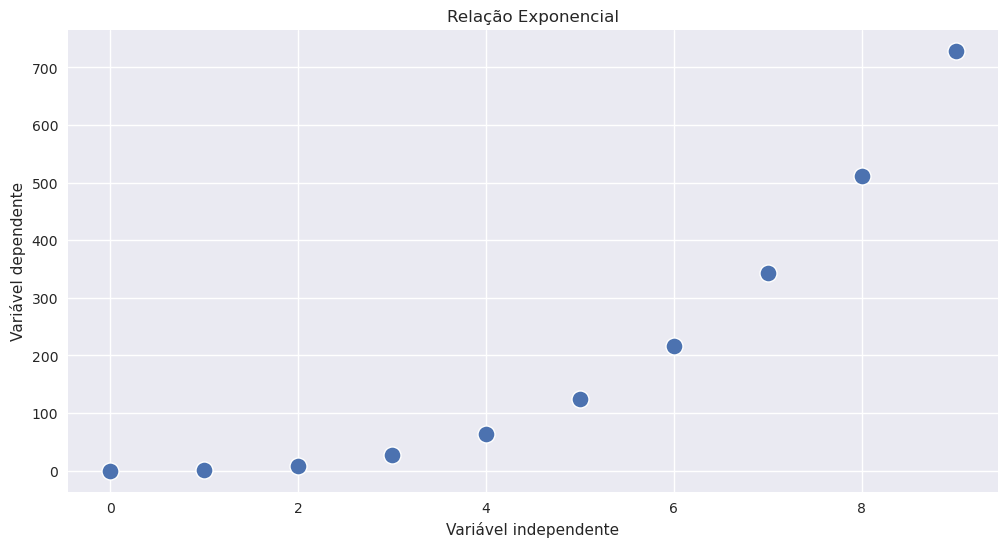
Pressuposto 2 - Homocedasticidade dos resíduos#
Uma análise entre taxa de juro de curto prazo e inflação. Podemos criar um modelo entre estas duas variáveis e se a análise tiver muitos anos podemos na realidade encontrar diferentes “períodos”. Diferentes lideranças do bancos centrais (assim como diferentes estados económicos) podem ter levado a um “regime shift” que vai invalidar uma análise que inclua todo o tempo.
É como se houvesse dois modelos diferentes. Um mais antigo e outro mais recente.
A variância dos resíduos neste caso é heterocedástica
(Exemplo na página 542)
Pressuposto 3: Independência#
Assumimos que as observações (pares Y e X) não estão correlacionadas entre si, ou seja, são independentes. Se houver correlação entre as observações (ou seja, autocorrelação), eles não são independentes e os resíduos serão correlacionados.
Autocorrelações dos retornos mensais do CSPX#
Show code cell source
tickers = ['CSPX.AS']
start = '2011-12-30'
end = '2021-12-31'
# Download das cotações
ETFs = download_yahoo_data(tickers=tickers, normalize_quotes=True, start=start, end=end)
# Fazer dataframe de retornos
ETFs_ret=ETFs.resample('M').last().pct_change().dropna() * 100
/tmp/ipykernel_158811/1727988276.py:9: FutureWarning: 'M' is deprecated and will be removed in a future version, please use 'ME' instead.
ETFs_ret=ETFs.resample('M').last().pct_change().dropna() * 100
Show code cell source
import statsmodels.api as sm
sm.graphics.tsa.plot_acf(ETFs_ret['CSPX.AS'], lags=10)
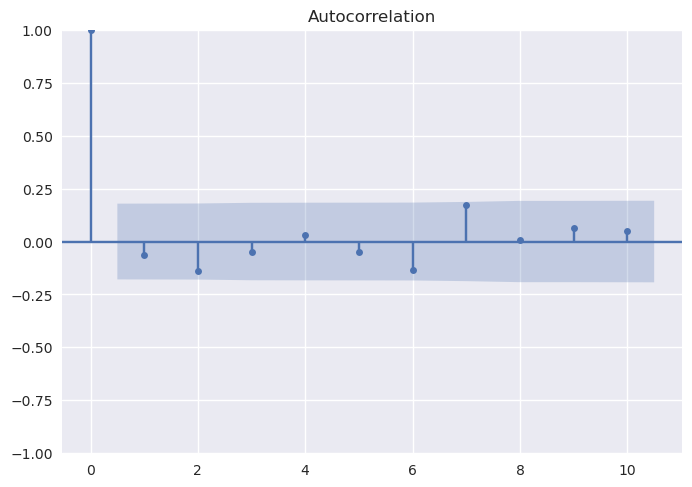

Pressuposto 4 - Normalidade#
Estamos a assumir que os resíduos são normalmente distribuídos.
Qualidade do modelo#
Coeficiente de determinação ou \(r^2\)#
O \(r^2\) é a percentagem da variação da variável independente que é explicado pela variável independente.
Exemplo com o ROA /CAPEX que fizemos acima (página 548)
Show code cell source
# Create the DataFrame
df = pd.DataFrame()
df['Y'] = [6.0, 4.0, 15.0, 20.0, 10.0, 20.0]
df['X'] = [0.7, 0.4, 5.0, 10.0, 8.0, 12.5]
# Set the plot size
plt.figure(figsize=(12, 6))
# Create the scatter plot with a regression line
sns.regplot(
data=df,
x='X',
y='Y',
scatter_kws={'s': 150}, # Marker size
line_kws={'color': 'black'}, # Trendline color
ci=None # Removes the confidence interval to mimic OLS trendline
)
# Set plot titles and labels
plt.title("Scatter plot ROA/CAPEX, com regressão linear OLS")
plt.xlabel("CAPEX (%)")
plt.ylabel("ROA (%)")
# Customize the y-axis range and add percentage formatting to both axes
plt.ylim(0, 22)
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda y, _: f'{y:.0f}%'))
plt.gca().xaxis.set_major_formatter(plt.FuncFormatter(lambda x, _: f'{x:.0f}%'))
# Show the plot
plt.show()

Calcular coeficientes
No resultado temos o rvalue. Por sua vez o \(R^2\) é naturalmente esse valor elevado ao quadrado.
# Python a saber
Y = [6.0, 4.0, 15.0, 20.0, 10.0, 20.0]
X = [0.7, 0.4, 5.0, 10.0, 8.0, 12.5]
compute_regression_coeficients(x=X, y=Y)
LinregressResult(slope=1.25, intercept=4.874999999999999, rvalue=0.894485541601211, pvalue=0.01611258928781205, stderr=0.31239805904148915, intercept_stderr=2.3719633958885398)
0.894485541601211**2
0.8001043841336117
Um \(r^2\) elevado normalmente significa que, pelo menos inicialmente, o modelo é explicativo. Olhando para os gráficos uma gráfico onde a linha de regressão linear é inclinada terá um \(R^2\) elevado e se for horizontal terá um \(R^2\) baixo, o que significa que o modelo não tem capacidade explicativa ou preditiva.
Fórmula a saber sobre o coeficiente de determinação#
Porque muitas vezes só têm acesso à Sum of Square regression e à sum of square total. Criei função compute_coefficient_of_determination só para se lembrarem. Vamos usar esta função para resolver exercícios.
Erro Padrão#
O erro padrão é medida da distância entre os valores observados da variável dependente e aquelas previstas a partir da regressão estimada; quanto menor o erro padrão melhor o ajuste do modelo.
Exercício (Exemplo 5 página 551)
1. Calcule o coefficiente de determinação deste modelo de regressão?
2. Qual é o erro padrão da estimativa para este modelo de regressão?
# squares regression/sum of squares total
compute_coefficient_of_determination(576.1485, 2449.7100)
0.23519049193578015
compute_std_error_reg(19.1180)
4.372413521157394









